Задача 29480 ...
Условие
б) Укажите корни этого уравнения, принадлежащие отрезку [π ; 5π/2].
Решение
cos(π-x)=-cosx
Замена переменной
16^(cosx)=t
16^(-cosx)=1/(16^(cosx))=1/t
Уравнение принимает вид
t+(1/t)=17/4;
4t^2-17t+4=0
D=289-4*4*4=289-64=225
t_(1)=(17-15)/8=1/4 или t_(2)=(17+15)/8=4
Обратная замена
16^(cosx)=1/4;
4^(2cosx)=4^(-1)
2cox=-1
cosx=-1/2
x= ± (2π/3)+2πk, k ∈ Z
ИЛИ
16^(cosx)=4
4^(2cosx)=4
2cosx=1
cos=1/2
x= ± (π/3)+2πn, n ∈ Z
а) О т в е т. ± (π/3)+2πn, n ∈ Z или ± (2π/3)+2πk, k ∈ Z
что можно записать короче так:
±( π/3)+πm, m ∈ Z
б) Указанному промежутку принадлежат три корня:
x_(1)=(-2π/3)+2π=4π/3;
x_(2)=(-π/3)+2π=5π/3
x_(3)=(π/3)+2π=7π/3
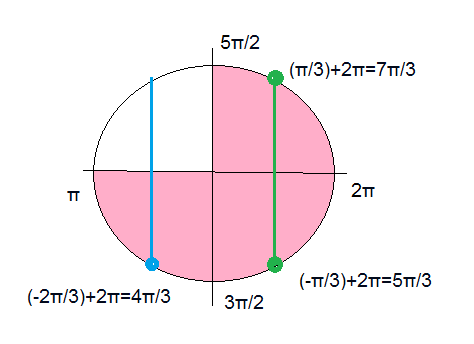
Все решения

