Задача 29438 ...
Условие
—каждый январь долг возрастает на 22% по сравнению с концом предыдущего года;
—с февраля по октябрь каждого года необходимо выплатить одним платежом часть долга;
—в ноябре каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите наименьшее значение S, при котором каждая из выплат будет
составлять целое число тысяч рублей.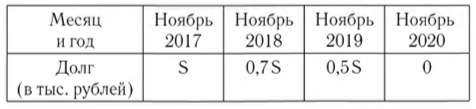
Решение
S; 0,7S; 0,5S; 0
По условию в январе следующего года долг увеличивается на 22%, значит
в январе 2018 года долг составит 1,22S;
в январе 2019 года долг составит 1,22*0,7S=0,854S;
в январе 2018 года долг составит 1,22*0,5S=0,61S.
Cледовательно, выплаты с февраля по октябрь каждого года:
1,22S-0,7S=0,52S;
0,854S-0,5S=0,354S;
0,61S
По условию числа
S; 0,52S; 0,354S и 0,61S - целое число тысяч рублей.
S; 13S/25; 48S/125;61S/100
S должно быть кратно
25;125 и 100
наименьшее общее кратное (25;125;100)=500
[b]S=500[/b]
Наименьшее целое число тысяч рублей при этом :
[b] 500 000[/b]
Проверка
0,52S=260 000 руб - целое число тысяч рублей
0,354S=177 000 руб.-целое число тысяч рублей
0,61S=305 000 руб. - целое число тысяч рублей
О т в е т. 500 000 руб.
