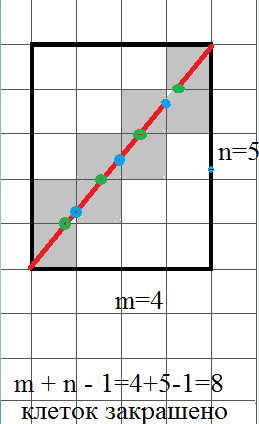
Задача 29403 14.8. На клетчатой бумаге выделен...

slava191

30 августа 2018 г. в 12:54

14.8. На клетчатой бумаге выделен прямоугольник размером mxn клеток, причем числа m и n взаимно простые и m < n . Диагональ этого прямоугольника не пересекает ровно 116 его клеток. Найдите все возможные значения m и n при данных условиях.

sova

30 августа 2018 г. в 15:48

★

Количество клеток, которые пересекает диагональ прямоугольника равно ( см. приложения)
(m + n – НОД(m,n))
Так как
НОД(m,n)=1,
то
количество клеток, которые пересекает диагональ прямоугольника равно
m+n–1
Уравнение:
m+n–1=mn–116
Решаем это уравнение в натуральных числах:
mn–m+n–1=116
m(n–1)+(n–1)=116
(n–1)·(m–1)=116

Раскладываем правую часть на множители и выбираем подходящие варианты:

116=2·58=2·2·29
m–1=1 ⇒ m=2
n–1=2·58⇒ n=117
или
m–1=2⇒m=3
n–1=58 ⇒ n=59
или
m–1=4⇒ m=5
n–1=29 ⇒ n=30
противоречие, m и n не взаимно простые.

аналогично не подходит вариант m–1=29; n–1=4

m–1=116 ⇒ m=117 > n не удовлетворяет условию

О т в е т. 2 и 117; 3 и 59