Задача 29200 ...
Условие
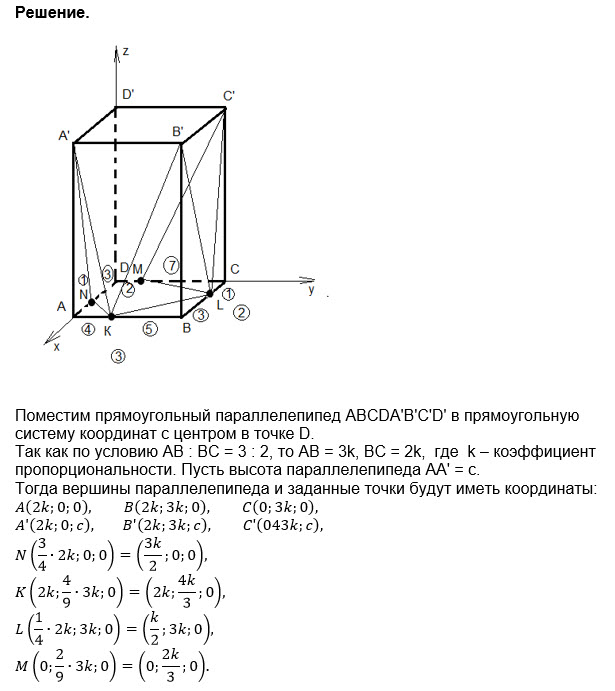
Решение
Такой тетраэдр называется [b] прямоугольным тетраэдром[/b]
К нему применимы методы, которые мы применяем к прямоугольному треугольнику.
В частности, достраиваем прямоугольный треугольник до прямоугольника. Диаметр окружности, описанной около прямоугольного треугольника - диагональ прямоугольника
Достраиваем тетраэдр BLKB' до параллелепипеда.
Значит [b] центр сферы, описанной около прямоугольного тетраэдра BLKB' - точка пересечения диагоналей K L' и K ' L прямоугольника KK'L'L. [/b] ( см. рис.1)
Q=K L' ∩ K ' L
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Q_(o) - проекция точки Q на плоскость основания ABCD.
KQ_(o)=Q_(o)L
Аналогично,
Тетраэдр CMLC' с вершиной в точке C, плоские углы при вершине - прямые. Значит центр сферы, описанной около тетраэдра - точка пересечения диагоналей прямоугольника
MM'L'L
R=M L' ∩ M ' L
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
R_(o) - проекция точки R на плоскость основания ABCD.
R_(o) - cередина LM.
Тетраэдр AKNA' с вершиной в точке A, плоские углы при вершине - прямые. Значит центр сферы, описанной около тетраэдра - точка пересечения диагоналей прямоугольника
KK'N'N
P=K N' ∩ K 'N
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
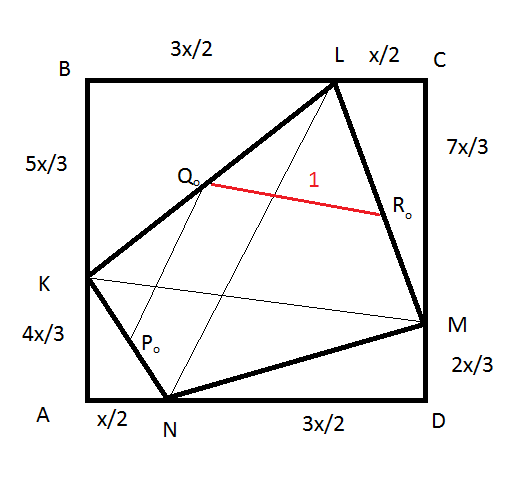
См. рис. 2
P_(o) - проекция точки P на плоскость основания ABCD.
KP_(o)=P_(o)N
P_(o) - cередина KN.
Q_(o)R_(o)=QR=1 ⇒ [b] KM=2 [/b]
По условию
AB:BC=3:2
Обозначим АВ=3х; ВС=2х
Так как
АК : КВ = 4 :5
AK=(3x/9)*4=4x/3
KB=(3x/9)*5=5x/3
Так как
BL : LC = 3 : 1
BL=(2x/4)*3=3x/2
LC=(2x/4)*1=x/2
Так как
СМ : MD = 7:2
СМ=(3х/9)*7=7х/3
MD=(3x/9)*2=2x/3
Так как DN:NA = 3:1
DN=(2x/4)*3=3x/2
NA=(2x/4)*1=x/2
Из прямоугольной трапеции АКMD
KM^2=AD^2+(AK-MD)^2
KM^2=(2x)^2+((4x/3)-(2x/3))^2
KM^2=40x^2/9
KM=2xsqrt(10)/3
Так как ранее было отмечено, что КМ=2QR=2
2x*sqrt(10)/3=2
x=3/sqrt(10)
Из прямоугольной трапеции LCDN:
LN^2=CD^2+(ND-LC)^2
LN^2=(3x)^2+((3x/2)-(x/2))^2
LN^2=10x^2
LN=x*sqrt(10)=(3/sqrt(10))*sqrt(10)=3
P_(o)Q_(o)=(1/2)LN=3/2=1,5
PQ=P_(o)Q_(o)=1,5
О т в е т. 1,5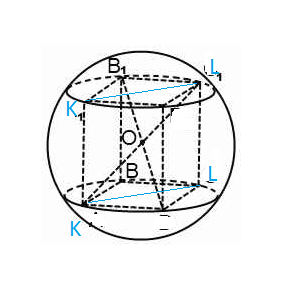
Все решения