Задача 29198 ...

slava191

8 февраля 2018 г. в 00:00

5. Дана трапеция ABCD с основаниями AD и ВС. Пусть М — середина отрезка AD, а N —произвольная точка отрезка ВС. Пусть К —пересечение отрезков СМ и DN, a L — пересечение отрезков MN и АС. Найдите все возможные значения площади треугольника DMК , если известно, что AD:ВС = 3:2, а площадь треугольника ABL равна 4.

SOVA

8 марта 2018 г. в 00:00

★

Δ LNC подобен Δ LMА по двум углам:
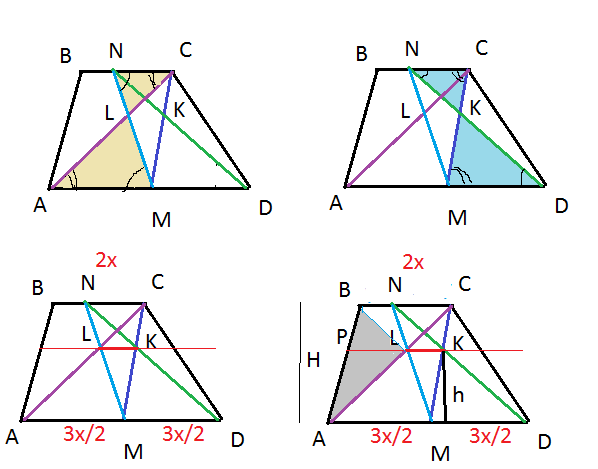
∠ LCN = ∠ LAM – внутренние накрест лежащие при BC||AD и секущей AC
∠ LNC = ∠ LMA – внутренние накрест лежащие при BC||AD и секущей MN

Из подобия следует пропорциональность сторон
NL : LM=NC:AM

Δ NKC подобен Δ DKM по двум углам:
∠ CNK = ∠ KDM – внутренние накрест лежащие при BC||AD и секущей ND
∠NCK = ∠ DMK – внутренние накрест лежащие при BC||AD и секущей CM

Из подобия следует пропорциональность сторон
NK : KD=NC:MD

Из полученных пропорций c учетом АМ=MD
NL : LM=NK : KD
По теореме, обратной теореме Фалеса, получаем, что
LK || AD
Но AD||BC
Значит,
LK || AD || BC

По условию AD:BC=3:2
Обозначим AD=3x; BC=2x
Тогда
AM=MD=3x/2

Обозначим высоту треугольника DMK через h.
Высоту трапеции через Н.
Δ APL подобен Δ ABC ( PL || BC)
PL : BC=h:H
PL=(h/H)·BC

Так как по условию

S( Δ ABL)=4

И с другой стороны
S( Δ ABL)=(1/2)PL·H,

4=(1/2)·(h/H)·BC·H

4=x·h

S(Δ DMK)=(1/2)·(3x/2)·h=(3/4)·(xh)=(3/4)·4=3

О т в е т. 3