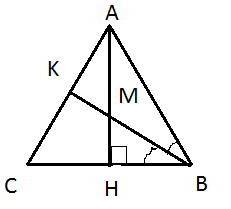
Задача 29173 Высота АН треугольника АВС пересекает...
Условие
ВМ:МК=2:1.
Найти АМ, если АВ=АС=21.
Решение
По условию АВ=АС, значит треугольник АВС – равнобедренный.
Высота АН является и биссектрисой и медианой этого треугольника.
По свойству биссектрисы угла треугольника: биссектриса АM треугольника АKВ делит сторону BК на отрезки, пропорциональные, прилежащим сторонам.
ВМ:МК=AВ:АК.
По условию задачи
ВМ:МК=2:1.
Следовательно,
AВ:АК=2:1.
АК=АВ/2
Так как АВ=АС,
То АК=АС/2 и точка К – середина АС
Значит ВК – медиана треугольника АВС
Биссектриса ВК делит сторону СА на отрезки, пропорциональные, прилежащим сторонам.
AK:КC=AB:BC.
АК=КС
АВ:ВС=1, АВ=ВС
Треугольник АВС – равносторонний
АН=АВ∙sin60° =21√3/2
АМ=(2/3)АН=7√3
О т в е т. 7√3
Ответ: 7√3