Задача 29167 16. В прямоугольном треугольнике ABC с...

u8418121178

8 января 2018 г. в 00:00

16. В прямоугольном треугольнике ABC с прямым углом C биссектриса BM и медиана AN пересекаются в точке E, при этом ME : BE = 5 : 9.
а) Докажите, что CM : AM = 4 : 5;
б) Найдите площадь треугольника ABC, если AC = 18.

SOVA

8 января 2018 г. в 00:00

★

а)
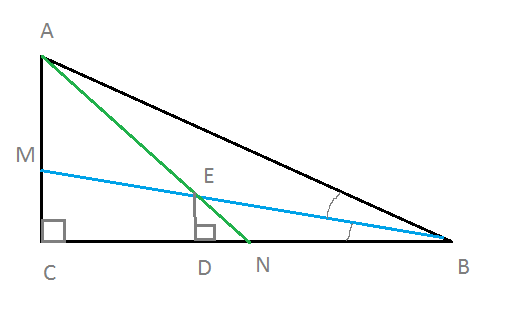
см. рис.
Проведем ED ⊥ BC
По теореме Фалеса
СD:DB=5:9
Обозначим коэффициент пропорциональности k, тогда
CD=5k
DB=9k
CB=CD+DB=5k+9k=14k
CN=NB=7k ( N – середина ВС)

Δ BMC подобен Δ BED
ED:MC=BD:BC=9:14
ED=(9/14) MC

Из подобия треугольников EDN и ACN:
ED:AC=DN:CN

(9/14)MC/(AM+MC)=2:7
Из пропорции
2АМ+2MC=(9/2)MC
AM=(5/4)MC
AM:MC=5:4

б)
АС=18
AM:MC=5:4
Биссектриса BM делит сторону АС на части, пропорциональные прилежащим сторонам треугольника,
значит АВ=5х, СВ=4х
По теореме Пифагора
AB²=AC²+BC²
(5x)²=18²+(4x)²
9x²=324
x²=36
x=6
BC=4x=4·6=24

S( Δ АВС)=(1/2)АС·BC=(1/2)·18·24=216
О т в е т. 216