Задача 29149 ...

slava191

31.07.2018

4.3.134) Показать, что фокус параболы и точки касания двух касатель­ных к параболе, проведенных из любой точки директрисы, ле­жат на одной прямой.

SOVA

01.08.2018

★

Парабола – геометрическое место точек, равноудаленных от данной прямой и данной точки, не лежащей на этой прямой. Прямая называется директрисой, точка F– фокусом параболы.
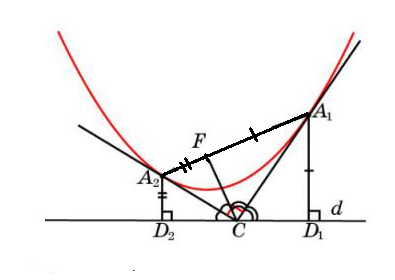
Cм. рис. 1

F – фокус параболы.
A_(1) и A_(2) – точки касания параболы
и касательных CA_(1) и СА_(2)
C принадлежит директрисе d.

A_(1)D_(1) ⊥ d, A_(2)D_(2) ⊥ d.

Треугольник FA_(1)D_(1) – равнобедренный (FA_(1)=A_(1)D
по определению параболы)
A_(1)C– высота, медиана и биссектриса равнобедренного треугольника.
∠ FA_(1)C = ∠D_(1)A_(1)C = альфа
тогда
∠ FCA_(1)=∠D_(1)CA_(1)= бета
альфа + бета =90 градусов

Аналогично, треугольник FA_(2)D_(2) – равнобедренный (FA_(2)=A_(2)D по определению параболы)
A_(2)C– высота, медиана и биссектриса равнобедренного треугольника.
∠ FA_(2)C = ∠D_(2)A_(2)C =
и
∠ FCA_(2)=∠D_(2)CA_(2)

Углы D_(2) СF и D_(1)C F - cмежные.
Их cумма 180 градусов.
Биссектрисы смежных углов образуют прямой угол.
∠ А_(2)CA_(1)= 90 градусов.

Значит,
∠ FCA_(2)=∠D_(2)CA_(2)=альфа
∠ FA_(2)C = ∠D_(2)A_(2)C = бета

CF ⊥ A_(1)A_(2)
CF- кратчайшее расстояние от С до A_(1)A_(2).
Значит, три точки A_(1), F и А_(2) лежат на гипотенузе прямоугольного треугольника A_(1)CA_(2)