Задача 29147 ...

slava191

31.07.2018

4.3.132) Из фокуса параболы у^2 = 12х под острым углом а к оси Ох направлен луч света. Известно, что tga = 3/4. Дойдя до пара­болы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

SOVA

31.07.2018

★

Каноническое уравнение параболы
y^2=2*px;
F(p/2;0) – фокус параболы.

В данном случае
2p=12
p=6
F(3;0)

Прямая, проходящая через точку F имеет угловой коэффициент k=3/4
Общее уравнение прямой с угловым коэффициентом k имеет вид:
y=kx+b
k=3/4
Для того чтобы найти b подставим координаты точки F
0=(3/4)*3+b
b=–9/4

Прямая, проходящая через фокус F под углом α ;
tg α =3/4 задается уравнением
y=(3/4)x – (9/4)

Находим точки пересечения этой прямой и параболы.
Решаем систему уравнений:
{y^2=12x ⇒ x=y^2/12
{y=(3/4)x–(9/4)
⇒ y=(3/4)*(y^2/12) – (9/4) ⇒
y^2–16y–36=0
D=(–16)^2–4*(–36)=256+144=400
y_(1)=–2 или y_(2)=18
x_(1)=(–2)^2/12=1/3 или x_(2)=18^2/12=27

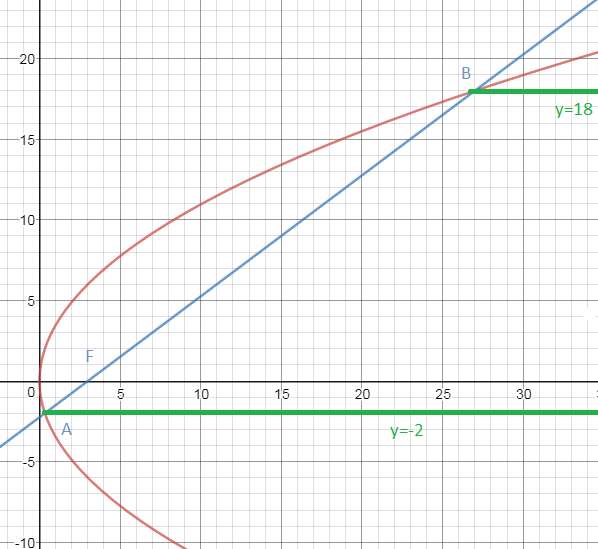
A(1/3;–2) и B(27;18)

Согласно оптического свойства параболы:
отраженный луч - прямая параллельная оси параболы.

Значит, уравнения прямых, на которых лежат отраженные лучи, имеют вид
y=-2 и у=18
О т в е т. y=-2; y=18