Задача 29145 ...

slava191

31 июля 2018 г.

4.3.130) Доказать оптическое свойство параболы: луч света, исходящий из фокуса параболы, отразившись от нее, идет по прямой, па­раллельной оси этой параболы.

SOVA

31 июля 2018 г.

★

По определению.
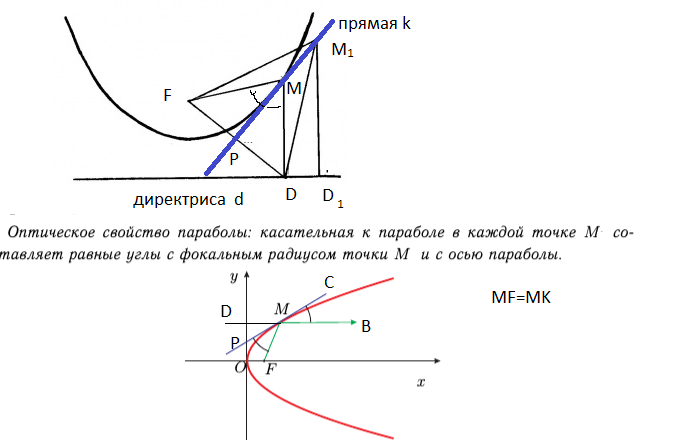
Парабола – геометрическое место точек, равноудаленных от данной прямой и данной точки, не лежащей на этой прямой. Прямая называется директрисой, а точка – фокусом параболы.
Cм. рис. 1

F – фокус параболы.
M – точка параболы
MD ⊥ d, d– директриса.

Треугольник FMD – равнобедренный (FM=MD по определению параболы)
MP– высота, медиана и биссектриса равнобедренного треугольника.
MP – серединный перпендикуляр к FD
MP – касательная к параболе.

Покажем, что M – единственная точка касания касательной и параболы, лежащая на биссектрисе MP.

Возьмем точку M₁, лежащую на биссектрисе MP
M₁ ≠ M
Проведем перпендикуляр M₁D₁ ⊥ d ( d – директриса)
FM₁=M₁D – по свойству серединного перпендикуляра
Но
M₁D > M₁D₁ ( наклонная больше перпендикуляра)
Значит,
FM₁ > M₁D и точка M₁ не принадлежит параболе.

Касательная к параболе МР – биссектриса ∠FMD

∠ FMP = ∠ MPD
∠ MPD = ∠ BMC – как вертикальные.

∠ FMP = ∠ BMC, значит касательная к параболе составляет равные углы с фокальным радиусом FМ и лучом МB, выходящим из точки M и сонаправленным с осью параболы.

Угол падения равен углу отражения, это означает, что луч направленный из фокального радиуса в точку M параболы, отразится в направлении луча MB,т.е по прямой параллельной оси Ох ( оси симметрии параболы)

Это и есть оптическое свойство параболы:
луч света, исходящий из фокуса параболы, отразившись от нее, идет по прямой, перпендикулярной директриcе и стало быть параллельной оси параболы.
См. рис.2