Задача 29117 9. Независимые случайные величины X и Y...
Условие
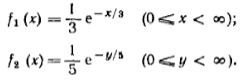
математика ВУЗ
4957
Решение
★
Z= X+Y, то z больше или равно 0
Применяем формулу
g(z)= ∫ ^(z)_(0)f_(1)xf_(2)(z-x)dx
Используя данные задачи
g(z)= ∫ ^(z)_(0)(1/3)*e^(-x/3)*(1/5)*e^(-(z-x)/5)dx=
=(-1/2)*e^(-z/5)*∫ ^(z)_(0)e^(-2x/15)d(-2x/15)=
=(-1/2)*e^(-z/5)*(e^(-2z/15)-e^(0))=
=(1/2)e^(-z/3)-(1/2)e^(-z/5)
О т в е т.
g(z)= (1/2) * (e^(-z/3)-e^(-z/5)) при z ∈ [0;+ бесконечность )