Задача 29112 2. Случайная'' величина X распределена...

slava191

28.07.2018

2. Случайная'' величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 6 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (4,8).

Отв. 0,6826.

SOVA

28.07.2018

★

Для нормально распределённой случайной величины вероятность попадания случайной величины Х в интервал (альфа; бета) находится по формуле:

P( альфа < x < бета )=
=Ф(( бета -a)/σ)-Ф(( альфа -a)/σ)
где Ф(x) - функция Лапласа

По условию
a=6
σ=2
альфа =4
бета =8

P( 4 < x < 8 )=Ф(( 8 -6)/2)-Ф(( 4 -6)/2)= Ф(1)-Ф(-1)
Так как функция Лапласа нечетная
Ф(-1)=-Ф(1)
Получаем
Ф(1) - Ф(-1) = Ф(1) - ( - Ф(1)) = 2Ф(1)
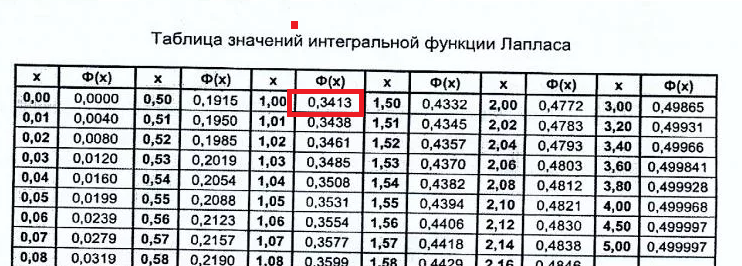
По таблице
Ф(1)=0,3413
( см. приложение)

О т в ет. 2*0,3413=0,6826