Задача 29100 16. В трапеции [m] ABCD [/m] точка [m] E...

u176594333

27 июля 2018 г.

16. В трапеции [m] ABCD [/m] точка [m] E [/m] – середина основания [m] AD [/m], точка [m] M [/m] – середина стороны [m] AB [/m].
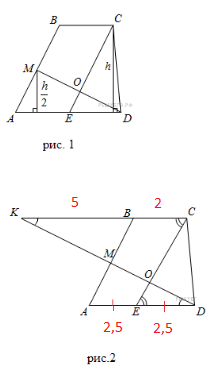
a) Докажите, что площади четырёхугольника [m] AMOE [/m] и треугольника [m] COD [/m] равны, если [m] O [/m] – точка пересечения отрезков [m] CE [/m] и [m] DM [/m].
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника [m] AMOE [/m], если [m] BC = 2 [/m], [m] AD = 5 [/m].

SOVA

27 июля 2018 г.

а)
Обозначим h – расстояние от точки С до AD, тогда
h/2 – расстояние от точки M до AD

S(Δ AMD) =(1/2)AD·(h/2)
S( Δ CED)= (1/2)ED·h=(1/2)·(AD/2)·h=(1/2)AD·(h/2)=S(Δ AMD)
Значит, S(Δ AMD)=S( Δ CED)

Так как
S(Δ AMD)= S (AMOE) + S (Δ OED)
S( Δ CED)= S ( Δ COD)+ S (Δ OED)
Левые части равны, приравниваем правые
S (AMOE) + S (Δ OED)=S ( Δ COD)+ S (Δ OED) ⇒
S (AMOE)=S ( Δ COD)

б)
Продолжим MD до пересечения с BC в точке К
Δ AMD и ΔBMK равны по
стороне ( АМ=МВ) и двум прилежащим к ней углам
∠ KMB=∠AMD – вертикальные
∠ KBM=∠MAD – внутренние накрест лежащие при параллельных прямых BC и AD и секущей АВ
Значит,
КB=AD=5
Δ KOC и OED подобны по двум углам.
∠ KOC=∠EOD – вертикальные
∠ KCO=∠EOD – внутренние накрест лежащие при параллельных прямых BC и AD и секущей CE

Из подобия следует пропорциональность сторон
CO:OE=KC:ED=(5+2):2,5=14:5

S( Δ CED) : S ( Δ EOD)=CE:OE=19:5

S( Δ COD)=(14/19)·S( Δ CED)
Так как
S( трапеции ABCD)=(BC+AD)·h/2=(2+5)·h/2=7h/2
S( Δ CED)=(1/2)ED·h=(1/4)AD·h=5h/4
то
S(AMOE)=S( Δ COD)=(14/19)·S( Δ CED)=
=14/19)·(1/2)ED·h=
=(14/19)·(5h/4)=(5/19)·(7h/2)=
=5/19) S( трапеции ABCD)
О т в е т. 5/19