Задача 29097 Все на картинке...
Условие
математика 10-11 класс
583
Все решения
cos^2x+15,25-cos2x=16
Подкоренное выражение равно 16, значит положительно, про ОДЗ можно ничего не говорить.
cos^2x - cos2x - (3/4)=0
Так как
cos2x=2cos^2x-1
cos^2=1/4
cosx=-1/2 или сosx=1/2
x= ± (2Pi/3)+2Pik, k ∈ Z или x= ± (Pi/3)+2Pin, n ∈ Z
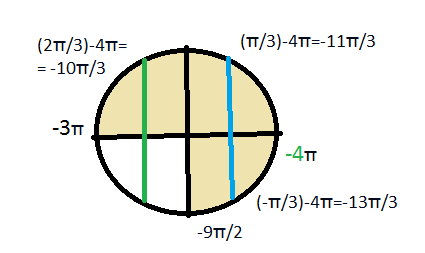
Указанному промежутку принадлежат корни ( см. рис.)
x_(1) = - (Pi/3) - 4Pi= -13Pi/3;
x_(2) = (Pi/3) - 4Pi= -11Pi/3;
x_(3)= (2Pi/3) - 4Pi = - 10 Pi/3.
