Задача 29071 7. Рукопись объемом в 1000 страниц...

slava191

24.07.2018

7. Рукопись объемом в 1000 страниц машинописного текста содержит 1000 опечаток. Найти вероятность того, что наудачу взятая страница содержит: а) хотя бы одну опечатку; б) ровно 2 опечатки; в) не менее двух опечаток. Предполагается, что число опечаток распределено по закону Пуассона.

SOVA

24.07.2018

★

Вероятность появления события А в одном испытании равна p.
Тогда вероятность появления события А в серии из n испытаний ровно m раз по формуле Пуассона:
P(m)=((лямбда )^(m)/m!)*e^(-лямбда)
лямбда=np (если n - велико, p очень мало)

В условии задачи нет ни n, ни p.

Но известно, что если случайная величина распределена по закону Пуассона, то математическое ожидание этой величины равно лямбда , впрочем как и дисперсия.
Дисперсия тоже равна лямбда

По условию среднее число опечаток на странице равно 1000/1000=1
Среднее число вызовов - это и есть математическое ожидание, поэтому
лямбда =1

а) Найдем вероятность противоположного события: ни одной опечатки на странице
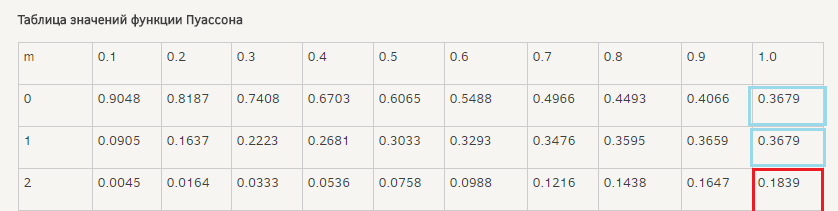
P(0)= ((1)^0/0!)*e^(-1) ≈0,3679
( cм . приложение. Таблица значений)

Тогда P(m > 0)=1 - P(0) ≈1 - 0,3679=0,6321


б)P(m=2)= ((1)^2/2!)*e^(-1) ≈ 0, 1839
( cм . приложение. Таблица значений)

в) Найдем вероятность противоположного события:
менее двух опечаток на странице ( одна или ни одной)
P(m < 2)=P(m=0)+P(m=1) =
= ((1)^0/0!)*e^(-1)+ ((1)^1/1!)*e^(-1)=

≈0,3679+0,3679=0,7358

Тогда P(m больше или равно 2)=1-P(m < 2)=
≈1- 0,7358=0,2642

О т в е т. а)≈ 0,6321; б)≈0,1839; в) ≈ 0,2642