Задача 29018 найдите наименьшее значение функции...
Условие
Все решения
Для нахождения производной применяем формулы
(u*v)`=u`*v+u*v`
и
(u^5)`=5u^4*u`
f `(x)=((0,4x+2)^5)`*(2x-3) + (0,4x+2)^5*(2x-3)`=
=5*(0,4x+2)^4*(0,4x+2)`*(2x-3)+(0,4x+2)^5*2=
=2*(0,4x+2)^4*(2,4x-1)
Так как (0,4x+2)^4 > 0 при любом х ≠ -5, то знак производной зависит от знака множителя (2,4x-1)
2,4x-1 > 0 при x > 5/12
2,4x - 1 < 0 при x < 5/12
При x=-5 f`(x)=0
Поэтому
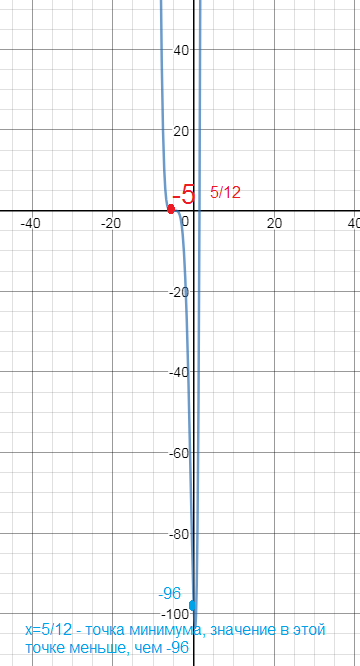
f `(x) меньше или равно 0 на (- бесконечность;0] , значит функция у=f(x) невозрастающая на (- бесконечность;0] и наименьшее значение принимает в точке x=0.
(cм. рис)
f(0)=2^5*(-3)=32*(-3)=-96
О т в е т. -96