Задача 29000 4.3.129) К параболе у^2 = 36х проведены...
Условие
Решение
Пусть (x_(o);y_(o)) - точка касания.
Уравнение касательной:
y-y_(o)=f`(x_(o))*(x-x_(o)).
Запишем уравнение параболы в виде:
y=6sqrt(x)
f(x)=6sqrt(x)
f`(x)=6/(2sqrt(x))=3/sqrt(x)
f`(x_(o))=3/sqrt(x_(o))
Точка касания лежит как на касательной, так и на параболе, поэтому
y_(o)=6sqrt(x_(o))
Уравнение касательной:
y - 6sqrt(x_(o)_=(3/sqrt(x_(o))*(x - x_(o))
Точка А (1;10) принадлежит касательной, значит ее координаты удовлетворяют уравнению касательной:
10 - 6sqrt(x_(o)) = (3/sqrt(x_(o))*(1 - x_(o))
или
3x_(o) - 10 sqrt(x_(o)) +3 =0
D=100-36=64
sqrt(x_(o))=1/3 или sqrt(x_(o))=3
x_(o)=1/9 или x_(o)=9
y_(o)=6*(1/3)=2 или y_(o)=6*3=18
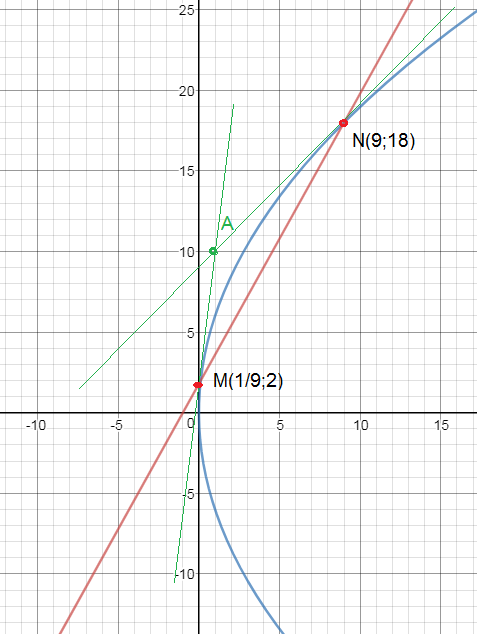
M(1/9; 2) и N (9;18) - точки касания.
Уравнение прямой MN как прямой
проходящей через две точки:
(х–x_(M))/(x_(N)–x_(M))=(y–y_(M))/(y_(N)–y_(M))
(x-(1/9))/(9-(1/9)) = (y - 2)/(18-2)
9x-1=5*(y-2);
9x-5y+9=0
О т в е т. 9x-5y+9=0