Задача 29 Прямая, параллельная гипотенузе АВ...

slava191

19.11.2013

Прямая, параллельная гипотенузе АВ прямоугольного треугольника ABC, пересекает катет АС в точке D, а катет ВС — в точке Е,причём DE = 2, a BE — 1. На гипотенузе взята такая точка F, что BF=1.Известно также, что ZFCB = а. Найдите площадь треугольника ЛВС.

Пусть Н — середина DE.
Тогда HFBE — параллелограмм (даже
ромб), т. к. НЕ =BF и НЕ \ BF.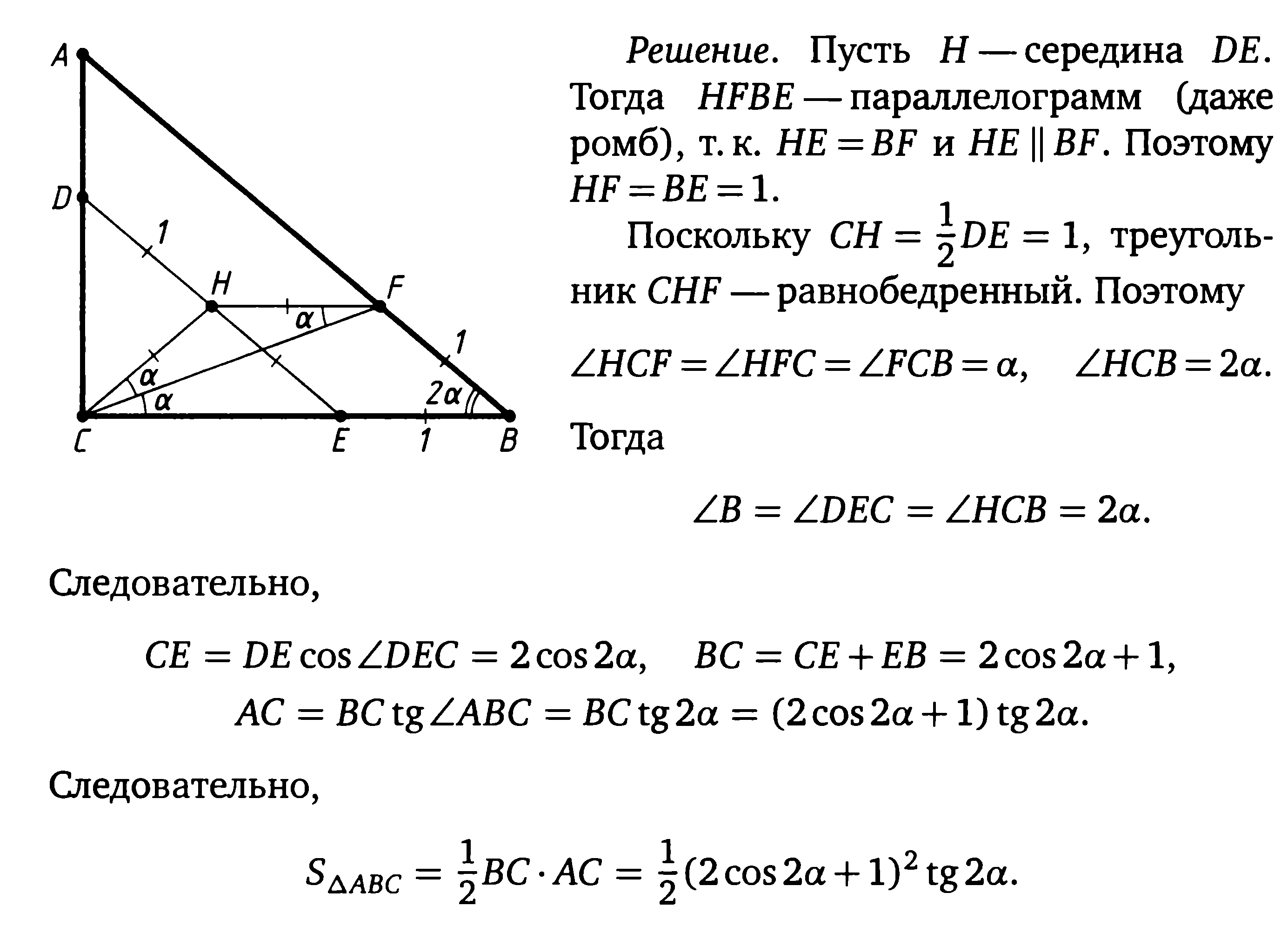

Ответ: в решение