Задача 28998 4.3.120) Парабола у^2 = х отсекает от...
Условие
координат, хорду, длина которой равна sqrt(2). Составить уравнение
этой прямой.
Решение
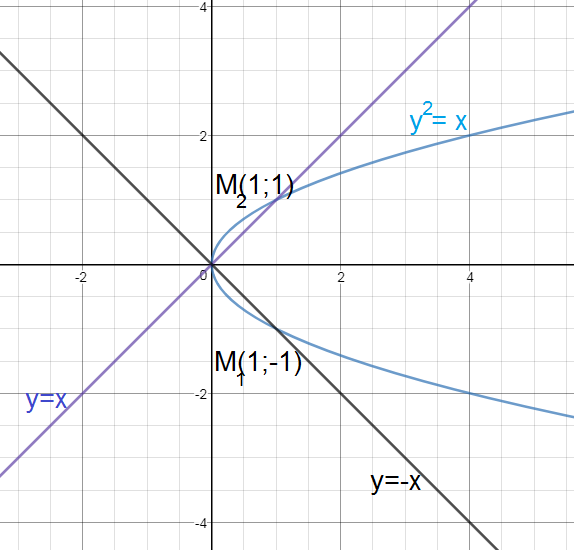
Парабола y^2=x расположена в правой полуплоскости,
[b] x больше или равно 0.[/b]
Пусть точка M(x;y) лежит на прямой.
О(0;0)
По условию
МО=sqrt(2)
sqrt(x^2+y^2)=sqrt(2)
или
x^2+y^2=2
Так как точка M(x;y) лежит и на параболе y^2=x, то заменим
y^2 на x:
x^2+x=2;
x^2+x-2=0
D=1^2-4*(-2)=1+8=9
x_(1)=(-1+3)/2=1 или x_(2)=(-1-3)/2= - 2
x_(2) не удовлетворяет условию x больше или равно 0 Точка с абсциссой х_(2) не лежит в правой полуплоскости.
Значит абсцисса точки пересечения прямой и параболы
х_(1)=1
Тогда
y^2=1
и получаем две точки
M_(1)(1;-1) и M_(2)(1;1)
Уравнение прямой ОM_(1) - уравнение биссектрисы второго и четвертого координатных углов
[b] y= - x [/b]
Уравнение прямой ОM_(2) - уравнение биссектрисы первого и третьего координатных углов
[b] y=x [/b]