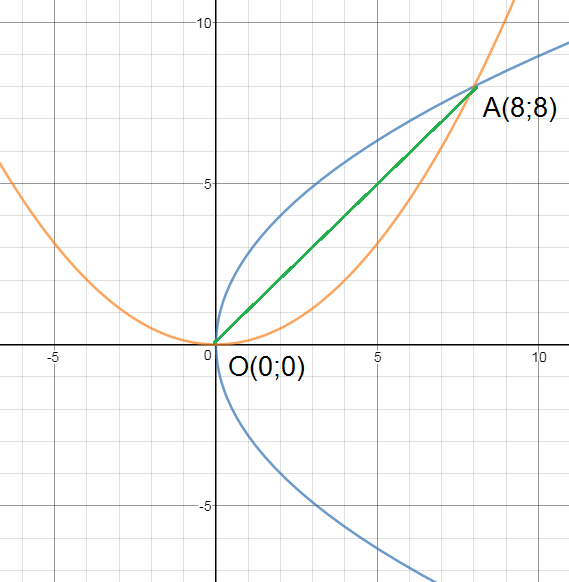Задача 28997 4.3.116) Найти длину хорды, соединяющей...

slava191

18.07.2018

4.3.116) Найти длину хорды, соединяющей точки пересечения двух парабол, имееющих общую вершину в начале координат, а фокусы
в точках (2; 0) и (0; 2).

SOVA

18.07.2018

★

Каноническое уравнение параболы, симметричной относительно оси Ох и имеющей фокус на оси Ох имеет вид:
y^2=2p_(1)x
F_(1)(p_(1)/2;0)

Каноническое уравнение параболы, симметричной относительно оси Оy и имеющей фокус на оси Оy имеет вид:
x^2=2p_(2)y
F_(2)(0; p_(2)/2)

Так по условию
F_(1)(p_(2)/2;0)=(2;0) ⇒ p_(1)/2=2 ⇒ p_(1)=4
F_(2)(0; p_(2)/2)=(0;2) ⇒ p_(2)/2=2 ⇒ p_(2)=4

Уравнения парабол имеют вид:
y^2=8x и x^2=8y

Находим точки пересечения парабол, решаем систему уравнений:
{y^2=8x;
{x^2=8y ⇒ y=x^2/8
и подставляем в первое уравнение:
(x^2/8)^2=8x;
x^4/64=8x
x^4=512x
x^4-512x=0
x*(x^3-512)=0
x_(1)=0 или x^3-512=0 ⇒ x_(2)=8
y_(1)=0 ; y_(2)=(x^2_(2))/8=8

Расстояние между точками O(0;0) и А (8;8)
OA=sqrt((8-0)^2+(8-0)^2)=sqrt(64+64)=8sqrt(2)

О т в е т. 8 sqrt(2)