Задача 28927 4.3.81) Найти расстояние между точками...

slava191

15.07.2018

4.3.81) Найти расстояние между точками пересечения асимптот гиперболы
9х^2-16у^2 = 144 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

SOVA

17.07.2018

★

Канонический вид гиперболы:
(x^2/a^2)-(y^2/b^2)=1

[b] Уравнения асимптот гиперболы имеют вид:[/b]

[b]y=(±b/a)x[/b]

[b]Фокусы гиперболы имеют координаты
F_(1)(-с;0) и F_(2)(с;0)
b^2=c^2-a^2[/b]


Разделим обе части уравнения на 144:
(9x^2/144)-(16у^2/144)=1
Канонический вид гиперболы:
(x^2/16)-(y^2/9)=1
a^2=16
b^2=9
Тогда
[b] уравнения асимптот гиперболы

y=(±3/4)x[/b]

c^2=b^2+a^2=9+16=25
[b]Фокусы гиперболы имеют координаты
F_(1)(-5;0) и F_(2)(5;0) [/b]

OF_(2)=5
R=OF_(2)=5

Уравнение окружности с центром в точке
F_(2) (5;0) и радиусом R=5 имеет вид

(x-5)^2+(y-0)^2=25;
(x-5)^2+y^2=25

Чтобы найти точки пересечения гиперболы
асимптоты y=(-3/4)x
и
окружности
(x-5)^2+y^2=25
решим систему уравнений:

{y=(-3/4)x
{(x-5)^2+y^2=25

Подставим y=(-3/4)x во второе уравнение
(х-5)^2+((-3/4)x)^2 = 25;

Упрощаем
x^2-10x+25+(9/16)x^2=25
(25/16)x^2-10x=0
x*((5/16)x-2)=0
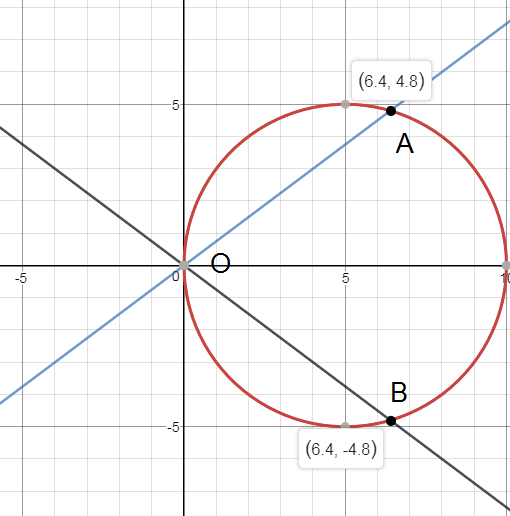
x_(1)=0 или x_(2)=(32)/5=6,4
y_(1)= (-3/4)*(6,4)=-4,8

Итак, асимптота y=(-3/4)x пересекается с окружностью
(х-5)^2+y^2=25 в точках
O(0;0) и А(6,4; - 4,8)
Аналогично, асимптота y=(3/4)x пересекается с окружностью (х-5)^2+y^2=25 в точках
O(0;0) и B(6,4; + 4,8)

ОА=ОВ=sqrt(6,4^2+4,8^2)=sqrt(40,96+23,04)=sqrt(64)=8
AB=2*4,8=9,6

О т в е т. 8; 9,6