Задача 28923 Докажите двумя способами, что...

u4614714047

15.07.2018

Докажите двумя способами, что неравенство x^2-4x+10 > 0 истинно при любом значении х: а) используя свойства графика функции y=x^2-4x+10;б) выделяя из трёхчлена x^2-4x+10 квадрат двучлена.

SOVA

15.07.2018

★

а) Графиком y=x^2-4x+10 является парабола
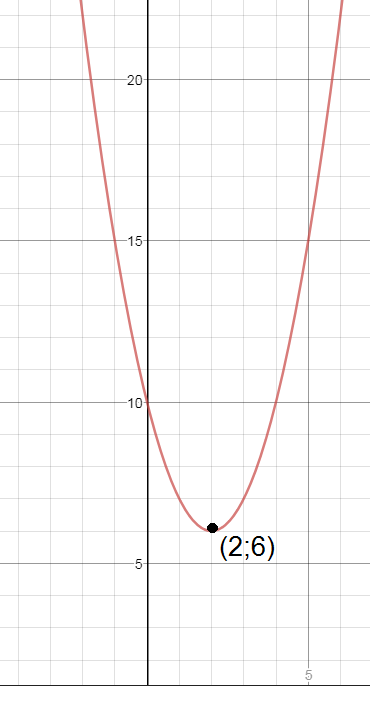
с вершиной в точке х_(o)= - b/2a= - (-4)/2=2
y_(o)=2^2-4*2+10=6

Парабола не пересекает ось Ох, так как уравнение
x^2-4x+10=0 не имеет корней,
D=(-4)^2-4*10 = 16-40 =- 24 < 0
Парабола расположена выше оси Ох ( см. рис.)
Поэтому неравенство x^2-4x+10 > 0 верно при любом х

б)
Выделяем полный квадрат
x^2-4x+10=x^2-4x+4+6=(x-2)^2+6
(x-2)^2 больше или равно 0 при любом х
(x-2)^2+6 > 0 при любом х