Задача 28921 ...

u4614714047

14.07.2018

Решите неравенство: 3x^2+7x-20≥0 двумя способами: а) используя свойства графика функции: y=3x^2+7x-20; б) разложив трёхчлен 3x^2+7x-20 на линейные множители и используя условие, при котором полученное произведение положительно.

SOVA

14.07.2018

★

a) Графиком функции является парабола, ветви которой направлены вверх. Вершина в точке
x_(o)=-b/2a=-7/(2*3)=-7/6
y_(o)=3*(-7/6)^2+7*(-7/6)-20=(147-294-720)/36=-867/36=
=-289/12
Найдем точки пересечения параболы с осью Ох
3x^2+7x-20=0
D=7^2-4*3*(-20)=49+240=289
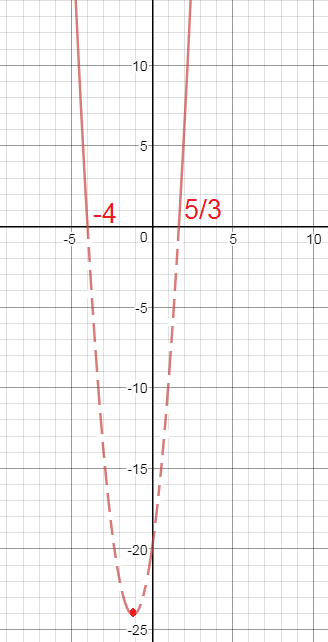
x_(1)=(-7-17)/6=-4 или x_(2)=(-7+17)/6=5/3
см. рисунок
Та часть параболы, которая не удовлетворяет неравенству изображена пунктиром.
О т в е т. (- бесконечность ;-4] U[5/3;+ бесконечность)

б)
Квадратный трехчлен раскладывается на множители по
формуле:
ax^2+bc+c=a*(x-x_(1))*(x-x_(2))
x_(1) и х_(2) найдены в пункте а)
3x^2+7x-20=3*(x-(-4))*(x-(5/3))=(3x-5)*(x+4)

3x^2+7x-20 больше или равно 0;
(3x-5)*(x+4) больше или равно 0

Произведение положительно ( неотрицательно), когда множители имеют одинаковые знаки.
(Оба больше или равно 0 или оба меньше или равно 0)

Получаем совокупность двух систем:
1)
{3x-5 больше или равно 0 ⇒ x больше или равно 5/3;
{x+4 больше или равно ⇒ x больше или равно -4
x больше или равно 5/3
2)
{3x-5 меньше или равно 0 ⇒ x меньше или равно 5/3;
{x+4 меньше или равно ⇒ x меньше или равно -4
x меньше или равно (-4)
Объединяем ответы 1) и 2) систем.
x меньше или равно (- 4) ИЛИ x больше или равно (5/3)
О т в е т.(- бесконечность ;-4] U [5/3; + бесконечность )