Задача 28901 8. Найдите все значения параметра а, при...
Условие
Решение
a=(x^4+10x^2+1)/(x^3+x)
Решим задачу графически.
Исследуем функцию
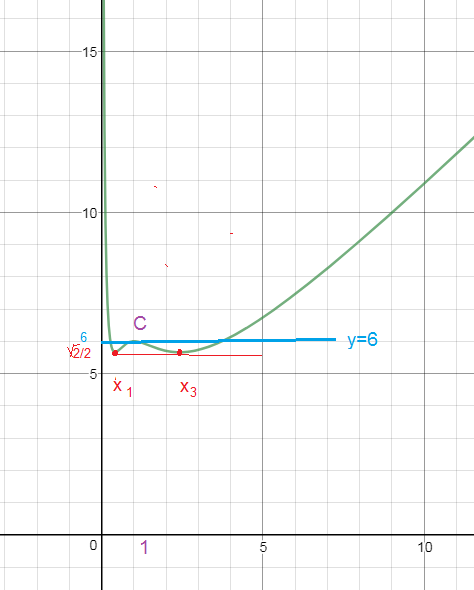
f(x)=(x^4+10x^2+1)/(x^3+x) и построим график.
Область определения (- бесконечность;0)U(0;+ бесконечность)
Функция нечетная, так
((-x)^4+10*(-x)^2+1)/((-x)^3+(-x))= - (x^4+10x^2+1)/(x^3+x)
Рассматриваем (0;+ бесконечность )
y`=((x^4+10x^2+1)*(x^3+x)-(x^4+10x^2+1)*(x^3+x)`)/(x^3+x)^2;
y`=((4x^3+20x)*(x^3+x)-(x^4+10x^2+1)*(3x^2+1))/(x^3+x)^2;
y`=(x-1)(x+1)*(x^4-6x^2+1)/(x^3+x)^2
y`=0
x=1 ; x=-1;
x^4-6x^2+1=0
D=36-4=32
x^2=3-2sqrt(2) или x^2=3+2sqrt(2)
Интервалу (0;+ бесконечность ) принадлежат три точки:
x_(1)=sqrt(3-2sqrt(2)); х_(2)=1; x_(3)= sqrt(3+2sqrt(2))
Знак производной:
(0) _-__ (x_(1)) __+__ (x_(2)) __-___ (x_(3)) __+__
x_(2)= 1 - точка максимума, производная меняет знак с + на -
f(1)=(1+10+1)/(1+1)=2
При a=2 уравнение имеет три корня.
При a > 2 уравнение имеет два корня.
( см. рис.)
x_(1) и x_(3) - точки минимума, производная меняет знак с - на +
Покажем, что значения функции в точках x_(1) и x_(3) равны.
f(x_(1))=((3-2sqrt(2))^2+10(3-2sqrt(2)+1)/(sqrt(3-2sqrt(2))*(3-2sqrt(2)+1)=
=8*sqrt(3-2sqrt(2))/(2-sqrt(2);
f(x_(3))=((3+2sqrt(2))^2+10(3+2sqrt(2)+1)/(sqrt(3+2sqrt(2))*(3+2sqrt(2)+1)=
=8*sqrt(3+2sqrt(2))/(2+sqrt(2);
f(x_(1))=f(x_(3)) так как
sqrt(3-2sqrt(2))/(2-sqrt(2)=sqrt(3+2sqrt(2))/(2+sqrt(2)
В самом деле, возводим обе части в квадрат
(3-2sqrt(2))/(4-4sqrt(2)+2)=(3+2sqrt(2)/(4+4sqrt(2)+2)
(3-2sqrt(2))/2*(3-2sqrt(3)=(3+2sqrt(2)/2*(3+2sqrt(2))=1/2
f(x_(1))=f(x_(3))=sqrt(2)/2
C учетом нечетности функции получаем
О т в е т. При a ∈ (- бесконечность;-6)U{-sqrt(2)/2}U{sqrt(2)/2}U(6;+ бесконечность)