Задача 28889 Задание № 12: Найти все значения...

vk195467882

10.07.2018

Задание № 12: Найти все значения параметра a, для которых прямые -4x + 6y = 1 и (6 + a)x + 2y = 3 не имеют общих точек.

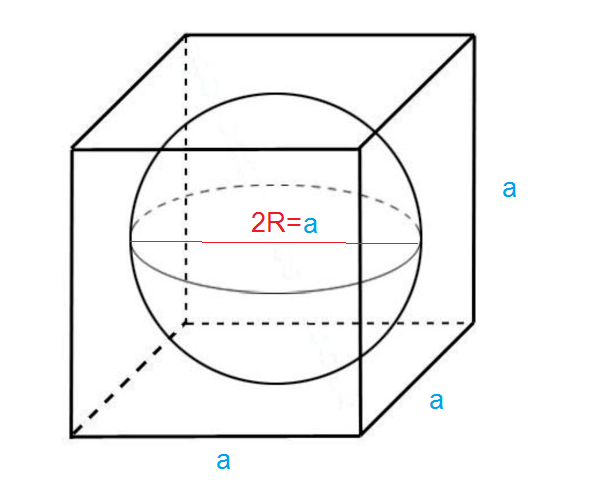
Задание № 13: Площадь сферы (в кв. см), вписанной в куб с диагональю 4 см равна

Задание № 14: Если число 1500 разделить на две части так, чтобы 4% первой части в сумме с 12% второй части составили 10,4% всего числа, то меньшая часть числа равна

SOVA

10.07.2018

12.
См. приложение 1.
- 4 / (6 + а) = 6/2 ⇒
6*(6 + a)=-4*2;
36 + 6a = - 8
6a = -8 -36
6a = - 44
a= -22/3

О т в е т. 2)

13.
См. рис. 2
Пусть сторона куба равна а
d^2=a^2+a^2+a^2
4^2=3a^2
[b]a^2=16/3[/b]
D( сферы) = а
D(сферы)=2R

S( сферы)=4Pi*R^2=PiD^2=Pia^2=Pi*(16/3)=16Pi/3
О т в е т. 2)

14.
Пусть одна часть х, вторая (1500 -х)
4%=0,04
12%=0,12
10,4%=0,104
Уравнение
0,04х +0,12*(1500-х)=0,104*1500;
0,04х +180 - 0,12х = 156
-0,08х= - 24
х=300
1500 - х =1500 - 300 = 1200

О т в е т. 5) 300