Задача 28885 Задание № 2: Знаменатель несократимой...

vk195467882

10.07.2018

Задание № 2: Знаменатель несократимой дроби на 2 больше, чем числитель. Если у дроби, обратной данной, уменьшить числитель на 3 и вычесть из полученной дроби данную дробь, то получится 1. Найдите эту дробь и в ответе укажите сумму ее числителя и знаменателя.

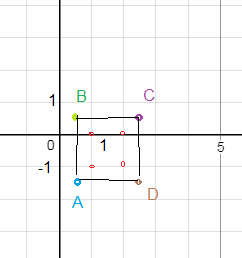
Задание № 3: Сколько точек (x, y) с целыми координатами x, y лежат внутри прямоугольника с вершинами A(0,5;–1,5), B(0,5;5,5), C(2,5;0,5), D(2,5;–1,5)?

SOVA

10.07.2018

1) x/(x+2) - данная дробь
(x+2)/x - обратная
((x+2)-3)/x =(х-1)/х

(х-1)/х - (х/(х+2)) = 1/15
Приводим к общему знаменателю 15*x*(x+2) и
приравниваем числители:

15*(x-1)*(x+2)-15x*x=x*(x+2)

x^2-13x+30=0
D=169-120=49
корни
3 и 10
Дробь
3/5 или (10/12) - не удовл условию: дробь должна быть нескоратимой.
3+5=8
О т в е т. 3)8.

2)См. рис.
О т в е т. 1) 4