Задача 28882 ...
Условие
Решение
sqrt(3)*|cosx|-sinx < sqrt (2)
Рассматриваем два случая:
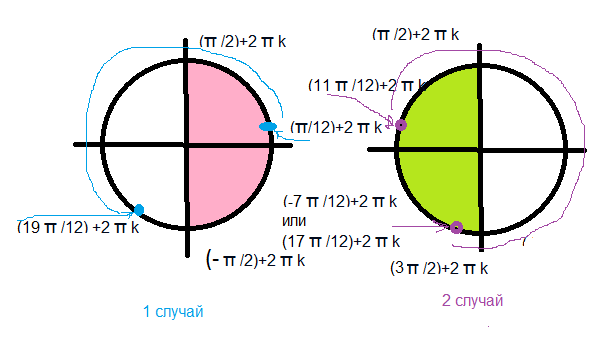
1)
cosx больше или равно 0
x ∈ [(-Pi/2)+2Pin;(Pi/2)+2Pin], n ∈ Z
sqrt(3)cosx-sinx < sqrt(2)
Применяем метод вспомогательного угла
Делим обе части неравенства на 2
(sqrt(3)/2)*cosx - (1/2)*sinx < sqrt(2)/2;
Пусть cos phi=sqrt(3)/2; sinphi=1/2
phi Pi/6
cos(Pi/6)*cosx-sin(Pi/6)sinx < sqrt(2)
cos(x+(Pi/6)) < sqrt(2)/2
(Pi/4)+2Pim < x+(Pi/6) < (7Pi/4)+2Pim, m ∈ Z
(Pi/4)-(Pi/6)+2Pim < x < (7Pi/4)-(Pi/6)+2Pim, m ∈ Z
(Pi/12)+2Pim < x < (19Pi/12) + 2Pim , m ∈ Z
C учетом x ∈ [(-Pi/2)+2Pin;(Pi/2)+2Pin], n ∈ Z
получаем ответ в первом случае
(Pi/12)+2Pim < x < (Pi/2) + 2Pim , m ∈ Z
2)
сosx < 0 ⇒ x ∈ ((Pi/2)+2Pik,(3Pi/2)+2Pik), k ∈ Z
Неравенство примет вид:
sinx > sqrt(3)*(-cosx) - sqrt(2)
sinx +sqrt(3)cosx > - sqrt(2)
Делим на 2
(1/2)*sinx + (sqrt(3)/2)*cosx > - sqrt(2)/2
sin(Pi/6)*sinx+ cos(Pi/6)*cosx > -sqrt(2)/2
cos(x-(Pi/6)) > -sqrt(2)/2
(-3Pi/4)+2Pin < x - (Pi/6) < (3Pi/4) + 2Pin, n ∈ Z
(-3Pi/4)+(Pi/6)+2Pin < x < (3Pi/4) +(Pi/6) + 2Pin, n ∈ Z
((-7Pi/12)+2Pin < x < (11Pi/12) + 2Pin, n ∈ Z
с учетом x ∈ ((Pi/2)+2Pik,(3Pi/2)+2Pik), k ∈ Z
получаем ответ второго случая
((Pi/2)+2Pik; (11Pi/12)+2Pik)U ((17Pi/12)+2Pik; (3Pi/2)+2Pik), k ∈ Z
О т в е т.
((Pi/12)+2Pik,(11Pi/12)+2Pik)U ((17Pi/12)+2Pik; (3Pi/2)+2Pik), k ∈ Z