Задача 28881 Все на картинке...
Условие
математика 10-11 класс
474
Все решения
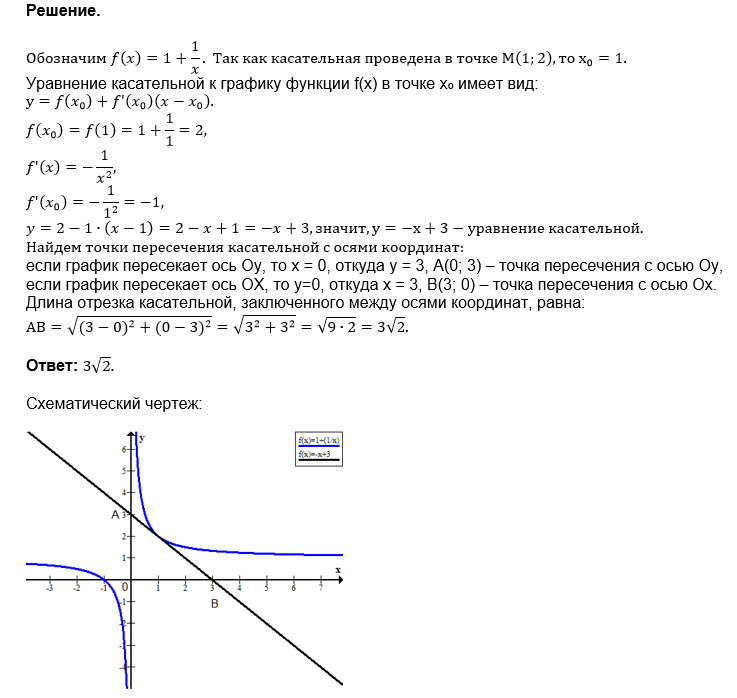
k( касательной)=f`(x_(o))
x_(o)=1
f`(x)=(1+(1/x))`=0-(1/x^2)
f`(x_(o))=f`(1)=-1
Уравнение касательной к кривой у=f(x) в точке (x_(o);y_(o))
имеет вид:
y-y_(o)=f`(x_(o))*(x-x_(o))
y-2 = -1* (x-1)
y=-x+3
Касательная пересекает оси координат в точках
A(0;3) и B(3;0)
По теореме Пифагора длина отрезка касательной - длина АВ равна
AB=sqrt(3^2+3^2)=sqrt(18)=3sqrt(2)
О т в е т. 3sqrt(2)
