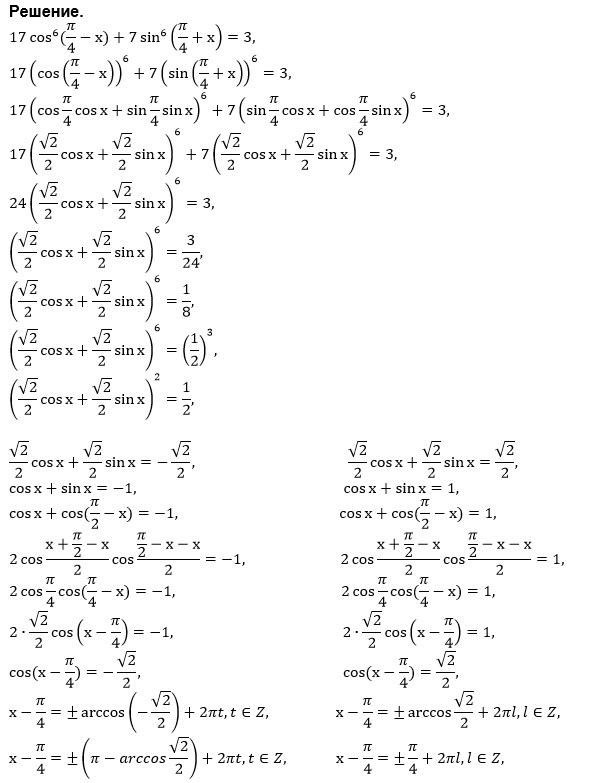Задача 28873 3. Решите уравнение...
Условие
17cos^6(Pi/4-x)+7sin^6(Pi/4+x) = 3
математика 10-11 класс
1535
Решение
★
cos^2 альфа =(1 + cos2 альфа )/2
sin^2 альфа = (1 - cos2 альфа)/2
cos^6((Pi/4)-x)=(cos^2((Pi/4)-x))^3
cos^2((Pi/4)-x)=(1+cos((Pi/2)-2x))/2=(1+sin2x)/2
cos^6((Pi/4)-x)=(1+sin2x)^3/8
sin^6((Pi/4)+x)=(sin^2((Pi/4)+x))^3
sin^2((Pi/4)+x)=(1-cos(Pi/2)+2x)/2=(1-(-sin2x))/2=(1+sin2x)/2
sin^6((Pi/4)+x)=(1+sin2x)^3/8
Уравнение принимает вид:
(17/8)*(1+sin2x)^3+(7/8)(1+sin2x)^3=3
((17/8)+(7/8))*(1+sin2x)^3=3
3*(1+sin2x)^3=3
1+sin2x=1
sin2x=0 ⇒ 2х=Pin, n ∈ Z ⇒x=(Pi/2)*n, n ∈ Z
О т в е т.(Pi/2)n, n ∈ Z
Все решения