Задача 28844 4. Меньший катет прямоугольного...
Условие
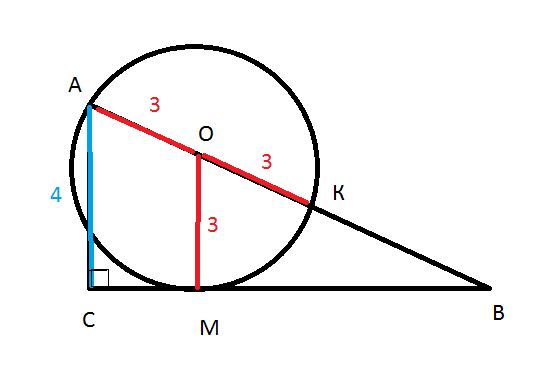
4. Меньший катет прямоугольного треугольника равен 4. Окружность радиуса 3 с центром на гипотенузе касается большего катета и проходит через вершину противоположного угла. Найдите гипотенузу.
предмет не задан
1284
Все решения
(ОМ ⊥ СВ ⇒ ОМ || АС)
Из подобия треугольников
следует пропорциональность сторон:
АС:ОМ=АВ:OВ [b](#)[/b]
По условию
АС=4; ОМ=AO=OB=r=3
тогда
АВ=АК+КВ=AO+OK+KB=r+r+КB=2r+KB=6+KB
[b] AB=6+KB[/b]
OB=OK+KB=r+KB=3+KB
[b]OB=3+KB[/b]
Подставляем в (#)
4:3=(6+KB):(3+KB)
Произведение крайних членов пропорции
равно произведению средних:
3*(6+КВ)=4*(3+КВ)ж
18+3КВ=12+4КВ;
КВ=6.
АВ=2r+KB=6+6=12
О т в е т. 12