Задача 28814 10.63) В основании прямой треугольной...
Условие
а) Докажите, что точка М — середина ребра СС1.
б) Найдите расстояние от точки А1 до плоскости APQ .
Решение
Пусть QF- средняя линия треугольника A1B1C1
QF=A_(1)C_(1)/2
[b] A_(1)C_(1)=2*QF [/b]
Так как по условию С_(1)P:PB_(1)=1:2
обозначим C_(1)P=x, тогда PB_(1)=2x
В_(1)С_(1)=3х
C_(1)F=FB_(1)=1,5x
PF=C_(1)F-C_(1)P=1,5x-x=0,5x
Продолжим A_(1)C_(1) до пересечения с QP в точке Т.
Треугольники FQP и ТС_(1)Р подобны по трем углам ( прямые QP и A_(1)T параллельны)
QF:C_(1)T=PF:C_(1)P=0,5x/x=1/2
C_(1)T=2QF
но так как [b]A_(1)C_(1)=2QF [/b], то
С_(1)Т=A_(1)C_(1)
Значит C_(1) - середина отрезка A_(1)T.
В треугольнике АА_(1)T
СС_(1) || AA_(1) и проходит через середину А_(1)Т
Значит, CМ- средняя линия треугольника АА_(1)Т
б)
Расстояние от точки А_(1) до плоскости АРQ - это высота пирамиды АА_(1)РQ.
Обозначим это расстояние Н.
V(пирамиды АА_(1)PQ)=(1/3)S( Δ APQ)
Значит,
[b]H=3V(пирамиды AA_(1)PQ)/S( Δ APQ) [/b]
Так как PQ:PT=PF:PC_(1)=1:2
V(пирамиды AA_(1)PQ)=(1/3)V(пирамиды АА_(1)QT)
V(пирамиды АА_(1)QT)=(1/3) S( ΔАА_(1)Т)*QE,
где QE || B_(1)C_(1) и QE=(1/2)B_(1)C_(1)=8
Найдем площадь прямоугольного треугольника АА_(1)Т. (AA_(1) ⊥ A_(1)C_(1))
АА_(1)=4sqrt(2)
A_(1)T=2A_(1)C=2*4=8
S(ΔАА_(1)Т)=(1/2)AA_(1)*A_(1)T=(1/2)*4sqrt(2)*8=
=16 sqrt(2)
V(пирамиды АА_(1)QT)=(1/3) *16sqrt(2)*8=
=128sqrt(2)/3
V(пирамиды AA_(1)PQ)=128sqrt(3)/3
Осталось найти площадь треугольника АРQ.
Из прямоугольного треугольника A_(1)B_(1)C_(1)
A_(1)B_(1)=sqrt(4^2+16^2)=sqrt(272)
Из прямоугольного треугольника АА_(1)Q:
A_(1)Q=QB_(1)=sqrt(272)/2=sqrt(68)=2sqrt(17)
Из прямоугольного треугольника AA_(1)T:
AT=sqrt(32+64)=sqrt(96)=4sqrt(6)
AQ=sqrt(AA^2_(1)+(A_(1)Q^2)=sqrt(32+68)=sqrt(100)=10;
[b] AQ=10[/b]
Из прямоугольного треугольника А_(1)B_(1)C_(1)
cos∠A_(1)=A_(1)C/A_(1)B_(1)=4/4sqrt(17)=1/sqrt(17)
Из треугольника А_(1)ТQ по теореме косинусов
QT=sqrt(8^2+68-2*8*2sqrt(17)*(1/sqrt(17)))=
=sqrt(64+68-32)=sqrt(100)=10
[b]QT=10[/b]
[b]AQ=QT=10[/b]
В равнобедренном треугольнике АQT
высота из вершины Q является одновременно и медианой.
QM=sqrt(AQ^2-AM^2)=sqrt(10^2-24)=sqrt(76)
S( Δ AQT)=(1/2)AT*QM=(1/2)*4sqrt(6)*sqrt(76)=
=4sqrt(6)*sqrt(19)
Так как треугольники АРQ и AQT имеют одинаковую высоту, проведенную из точки А, то их площади относятся как стороны, на которую проведена такая высота.
PQ=(1/3)TQ
и
S(Δ APQ)=(1/3)S(Δ AQT)=(4sqrt(6)*sqrt(19))/3
О т в е т.
[b]H=3V(пирамиды AA_(1)PQ)/S( Δ APQ) [/b]=
=128sqrt(2)/(4*sqrt(6)*sqrt(19))=32/sqrt(57)=32sqrt(57)/57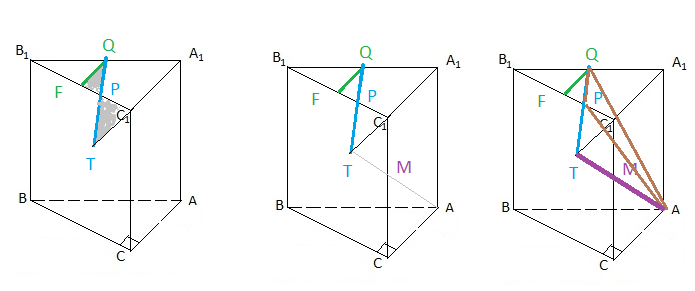
Все решения
призмы А(о;о;о), А1(о;о;4 sqrt(2)); Р(16/3;4; 4 sqrt(2)),G(8;2;4 sqrt(2)) Плоскость проходящая через точку М(x0:Y0:Z0) можно записать в виде а(x-x0)+b(y-y0)+c(z-z0)=0. Плоскость(АРG) проходит через точку А(о;о;о),поэтому ее уравнение имеет вид ах+ву+сz=0. Подставляя сюда координаты точек P и G получаем систему {16а/3+4в+4sgrt((2)c=0
{ 8а+2в+4sgrt(2)с=0, откуда находим , что в=4а/3; с=-4sgrt(2)а/3. Значит ,уравнение плоскости (АРG) имеет вид: ax+4ay/3-4sgrt(2)az/3=0. Учитывая что а ≠ 0 (иначе все три коэффициента обращаются в нуль),и сокращая , получаем уравнение 3x+4y-4sgrt(2)z=0. Расстояние от точки М0(x0y0z0) до плоскости , опредделяемой уравнением Ax+By+Cz+D=0 .находим по формуле
d=(|Ax0+By0+cz0+D|)/sgrt(A^2+B^2+C^2) :
В нашем случае А1(0;0;4sgrt(2)); получаем искомое расстояние d=(0+0+4sgrt(2)*4sgrt(2)|)/sgrt(3^2+4^2+(4sgrt(2))^2=32/sgrt(57).
Ответ: 32sgrt(57)/57.
