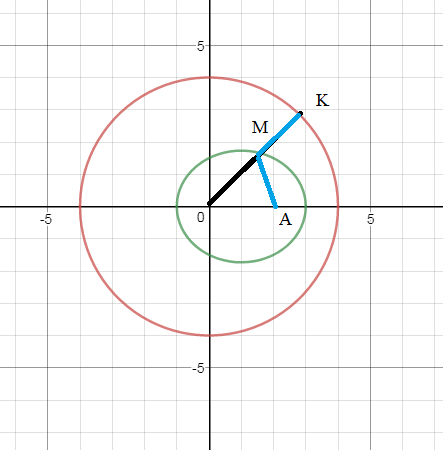
Задача 28812 4.3.44) Определить траекторию...

slava191

05.07.2018

4.3.44) Определить траекторию перемещения точки M, которая при
своем движении остается одинаково удаленной от точки А (2; 0)
и от окружности x^2+y^2=16.

SOVA

06.07.2018

★

Пусть M(x;y)
ОК=R=4
OM= sqrt(x^2+y^2)
MK=OK-OM=4-sqrt(x^2+y^2)

МА=sqrt((x-2)^2+(y-0)^2)

По условию
[b] МА=МК [/b]

sqrt((x-2)^2+y^2)=4-sqrt(x^2+y^2) (#)
4-sqrt(x^2+y^2) больше или равно 0 ⇒
sqrt(x^2+y^2) меньше или равно 4 ⇒
x^2+y^2 меньше или равно 16 ⇒ ⇒
Точка М(х;у) расположена внутри области, ограниченной данной окружностью.

Возводим обе части уравнения (#) в квадрат

(x-2)^2+y^2=16 - 8*sqrt(x^2+y^2)+x^2+y^2

8sqrt(x^2+y^2)=12+4x
2sqrt(x^2+y^2)=3+x
x больше или равно - 3
4*(x^2+y^2)=9+6x+x^2
3x^2-6x-9+4y^2=0
3(x^2-2x+1)+4y^2=12
О т в е т. эллипс ((x-1)^2/4) +(y^2/3)=1