Задача 28704 ...
Условие
2) y' - y * tg (x) = cos (x) * y^2
3) Решить интеграл ∫ 1 / √(3x^2 - 4x + 3)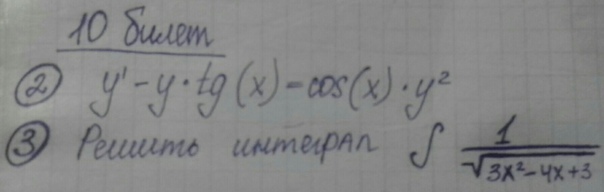
Все решения
Решаем однородное уравнение:
(1/y^2)y`-(1/y)tgx=0
Это уравнение с разделяющимися переменными
dy/y=dxtgx
Интегрируем
∫ dy/y=- ∫ d(cosx)/cosx
ln|y|=-ln|cosx|+lnC
y=C/cosx
Применяем метод вариации произвольной постоянной
y(x)=C(x)/cosx
y`(x)=(C`(x)*cosx-C(x)*(cosx)`)/cos^2x
y`=(C`(x)*cosx+C(x)*sinx)/cos^2x
Подставляем y и y` в данное уравнение
((C`(x)*cosx+C(x)*sinx)/cos^2x)-(C(x)/cosx)*tgx=
=cosx*(C^2(x)/cos^2x)
C`(x)/cosx=C^2(x)/cosx
C`(x)=C^2(x)
dC(x)/C^2(x)=dx
Интегрируем
-1/С(x)=x+c
C(x)=-1/(x+c)
О т в е т. y=-1/((x+c)*cosx) - общее решение данного уравнения
2.
Выделяем полный квадрат
3*(x^2-(4/3)x+1)=3*((x-(2/3))^2+(5/9))
Замена переменной
x-(2/3)=t
dx=dt
∫ dx/sqrt(3x^2-4x+3)= ( 1/sqrt(3))* ∫ dt/sqrt(t^2+(5/9))=
=(1/sqrt(3))*ln|t+ sqrt(t^2+(5/9))|+C=
=(1/sqrt(3))*ln|(x-2/3)+sqrt(x^2-(4/3)x+1)|+C