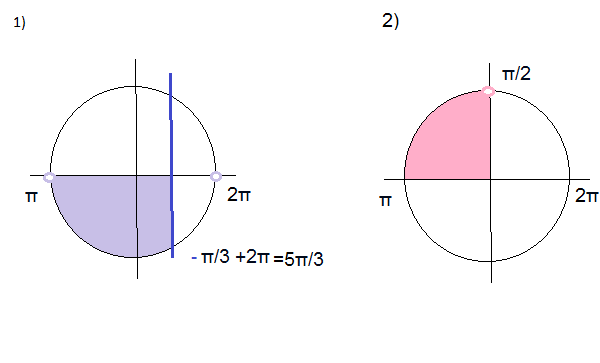Задача 28664 Все на картинке...
Условие
428
Решение
★
1-2cosx больше или равно 0 ⇒ cosx меньше или равно 1/2
1)
Если sinx < 0 - неравенство верно при любом х из ОДЗ
{sinx < 0
{cosx меньше или равно 1/2
см. решение на рис.1
2)
Если sinx больше или равно 0, обе части неравенства в квадрат
1 - 2cosx > sin^2x
1 - 2cosx > 1-cos^2x
cos^2x-2cosx > 0
cosx*(cosx-2) > 0
Так как |cosx| меньше или равно 1 ⇒ cosx-2 < 0, значит и второй множитель отрицателен
{sinx больше или равно 0
{cosx < 0
см. решение на рис.2
О т в е т.( (PI/2)+2Pik, (5Pi/3)+2Pik], k ∈ Z