Задача 28660 К графику функции y = x^2/2 проведены...

u18816222844

25 июня 2018 г.

К графику функции y = x²/2 проведены касательные, проходящие через точку M(1/2, –1). Найдите площадь четырехугольника, образованного этими касательными и осями координат.

SOVA

25 июня 2018 г.

f(x)=(x²/2)
f(x_o)=(x²_o/2)

f`(x)=x
f`(x_o)=x_o

Уравнение касательной
у – f(x_o)=f`(x_o)·(x – x_o)

y – (x²_o/2)=x_o·(x–x_o)

Подставляем координаты точки М в это уравнение:
х=1/2; у=–1
–1 – (x²_o/2)=x_o·((1/2) –x_o)

Решаем квадратное уравнение
х²_o–x_o–2=0
D=1–4·(–2)=9
x_o=–1 или х_o=2

Уравнение касательной в точке x_o=–1
у–(1/2)=–1·(х–(–1))
у=–х–(1/2)

Уравнение касательной в точке x_o=2
у–(2)=2·(х–2)
у=2х–2

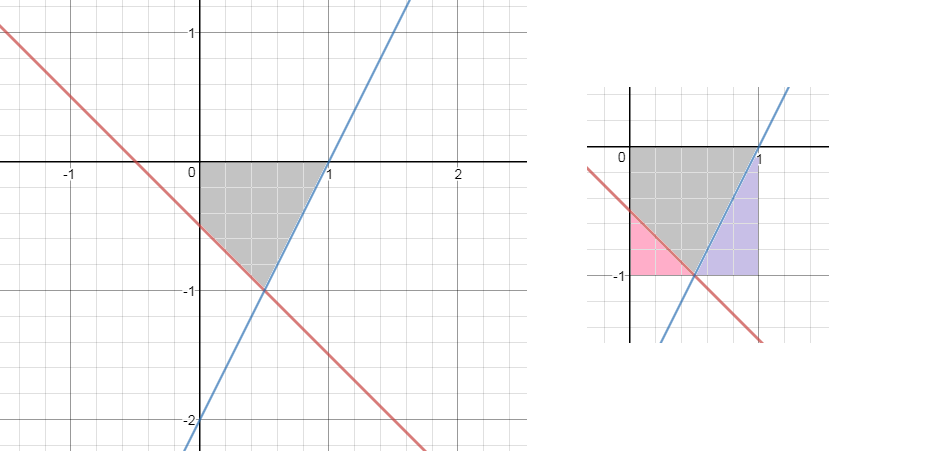
Фигура, ограниченная этими касательными и осями координат на рисунке.

S=S(квадрата 1×1)–S(розового треугольника)–S(сиреневого треугольника)=
=1·1–(1/2)·(1/2)·(1/2)–(1/2)·(1/2)·1=1–(1/8)–(1/4)=5/8