Задача 28626 2. Исследовать функцию на...

u8514079212

23 июня 2018 г.

2. Исследовать функцию на экстремум:
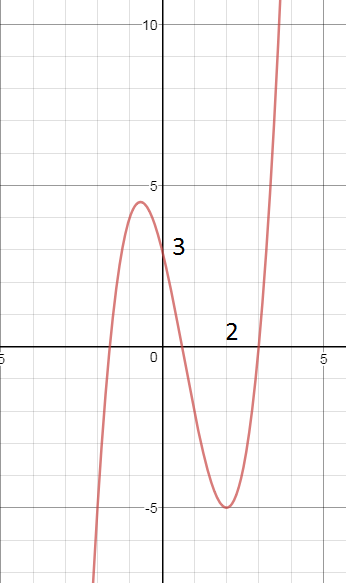
[m]f(x) = x^3 - 2x^2 - 4x + 3[/m]

3. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите [m] \frac{V}{\pi} [/m]

SOVA

23 июня 2018 г.

2.
D(y)=(– ∞ ;+ ∞ )
f`(x)=(x<sup>3</sup>–2x<sup>2</sup>–4x+3)`=3x²–4x–4
f`(x)=0
3x²–4x–4=0
D=(–4)²–4·3·(–4)=16+48=64
x=(4–8)/6=–2/3 или х=(4+8)/6=2
__+_–2/3 ___–__ (2) __+__

х= – 2/3 – точка максимума, производная меняет знак с + на –
х=2 – точка минимума, производная меняет знак с – на +

Функция возрастает на (– ∞;–2/3) и на (2;+ ∞); убывает на (–2/3;2).

См. график на рисунке.

3.
V(части цилиндра)=(1/4)V(цилиндра)=(1/4)·π·R²·H
R=6
H=5
V(части цилиндра)=45 π
О т в е т. 45