Задача 28621 ...

vk328058556

22 июня 2018 г.

1. Даны числа z₁ = – 1 + i, z₂ = 3 – 3i.
Вычислите разность и частное комплексных чисел z₁ и z₂.

3. Данo: 180° < α < 270°. Найдите sin α; cос α; tg α, если
cos α = – 3/5

4. Решите уравнение: tg² x + 4 tg x + 3 = 0.

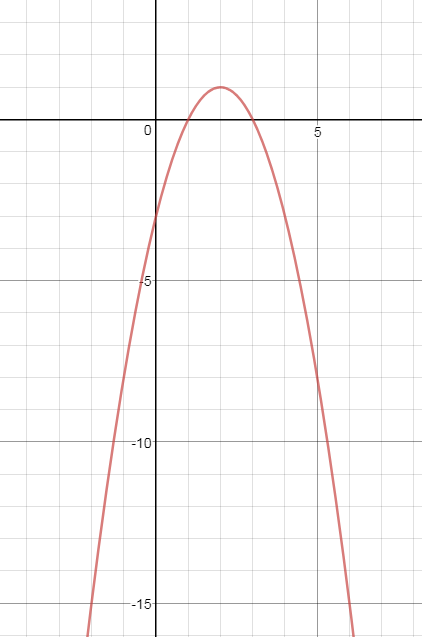
5. Постройте график функции y = – x² + 4x – 3 и укажите область определения и область значений.

SOVA

22 июня 2018 г.

2.
z₁ – z₂=(–1+i) – (3–3i)=–1 + i –3 +3i =
=(–1 – 3)+(i +3i)=– 4 + 4i

z₁/z₂=(–1+i)/(3–3i)=
умножаем и числитель и знаменатель на (3+3i)
=(–1+i)·(3+3i)/(9–(3i)²)=(–3+3i–3i+3i²)/18=–1/3

3.
Так как
sin² α +cos² α =1, то

sin α = ± √1– cos² α

По условию
180° < α < 270°
это третья четверть.
синус в третьей четверти имеет знак минус:
sin α = – √1 – cos² α = – √1–(–3/5)²=
= – √1 – (9/25)= – √16/25 = – 4/5
tg α =sin α /cos α = 4/3
ctg α =1/tg α =3/4

4.
Квадратное уравнение
tg²x+4tgx+3=0
D=(4)²–4·3=16–12=4
tgx= – 1 или tgx= – 3
x= ( – π/4)+πk, k ∈ Z или x=arctg(–3)+πn, n ∈ Z
О т в е т. (–π/4)+πk, – arctg3+πn, k, n ∈ Z

5.
y=–(x–2)²+1 – парабола, ветви вниз, вершина в точке (2;1)
cм. рис.
D(y)=(– ∞ ;+ ∞)
E(y)=(– ∞ ;+1)