Задача 28612 ...

vk328058556

22 июня 2018 г.

sin α = – 12/13.
3. Дано: 180° < α < 270°. Найдите cos α; c tg α; tg α.

4. Решите уравнение: tg² x – 4 tg x + 3 = 0.

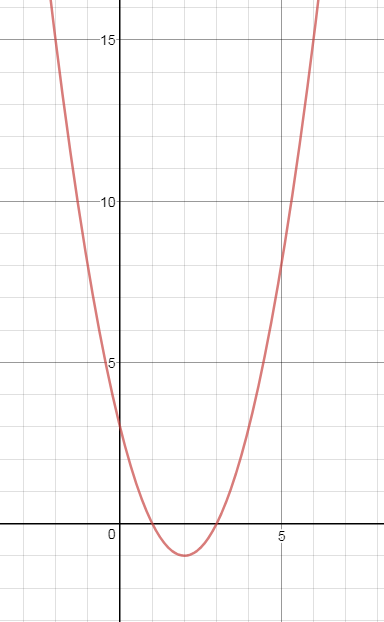
5. Постройте график функции y = x² – 4x + 3 и укажите ее свойства.

SOVA

22 июня 2018 г.

1.
Так как
sin² α +cos² α =1, то

сos α = ± √1–sin² α

По условию
180° < α < 270°
это третья четверть.
косинус в третьей четверти имеет знак минус:
сos α =–√1–sin² α =–√1–(–12/13)²=
=–√1–(144/169)=– √25/169=–5/13
tg α =sin α /cos α = 5/12
ctg α =1/tg α =12/5=2,4

2.
Квадратное уравнение
tg²x–4tgx+3=0
D=(–4)²–4·3=16–12=4
tgx=1 или tgx=3
x= (π/4)+πk, k ∈ Z или x=arctg3+πn, n ∈ Z
О т в е т. (π/4)+πk, arctg3+πn, k, n ∈ Z

3.
y=(x–2)²–1 – парабола, ветви вверх, вершина в точке (2;–1)
cм. рис.