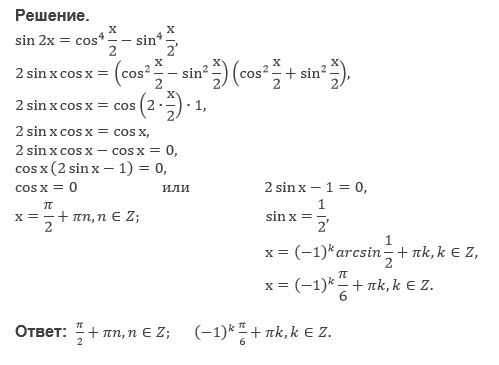Задача 28432 Sin2x=cos^4x/2-sin^4x/2...

u21387122217

12.06.2018

Sin2x=cos^4x/2-sin^4x/2

vk397114329

12.06.2018

Решение:
sin2x=2sinxcosx;
cos^4(x/2)-sin^4(x/2)= ((cos^2(x/2)-sin^(x/2)*((cos^2(x/2) +sin^2(x/2)) =cosx
cosx= cos^2(x/2)-sin^2(x/2
Подставим в исходное уравнение:
2sinx*cosx=cosx;
cosx(2sinx-1)=0;
cosx=0. x=pi/2+pi*k.k- целые числа.
2sinx-1=0; sinx=1/2. Отсюда x= (-1)^k*pi/6+pi*k. k-целые числа