Задача 28411 Провести полное исследование функций,...

vk445839739

6 октября 2018 г. в 00:00

Провести полное исследование функций, построить их графики

Вариант 19

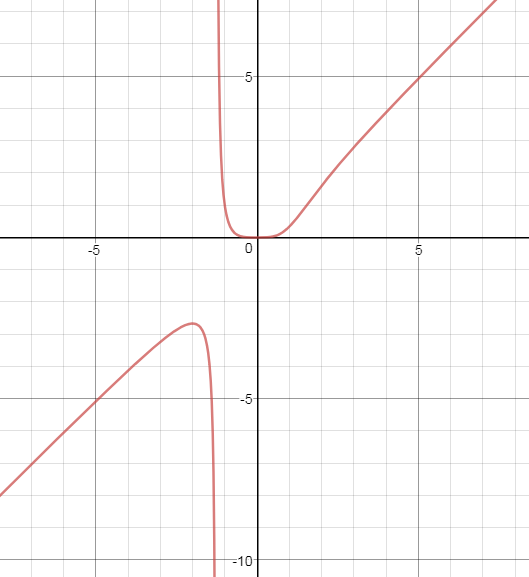
1) y = x⁴ / x³ + 1

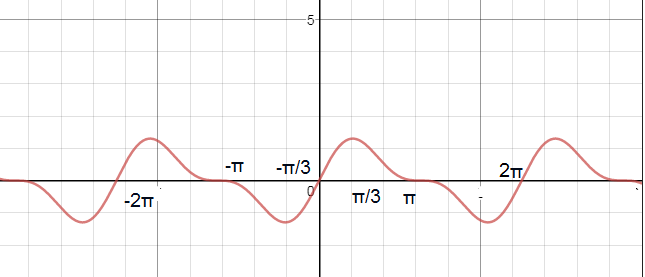
2) y = sin x + 1/2 sin 2x

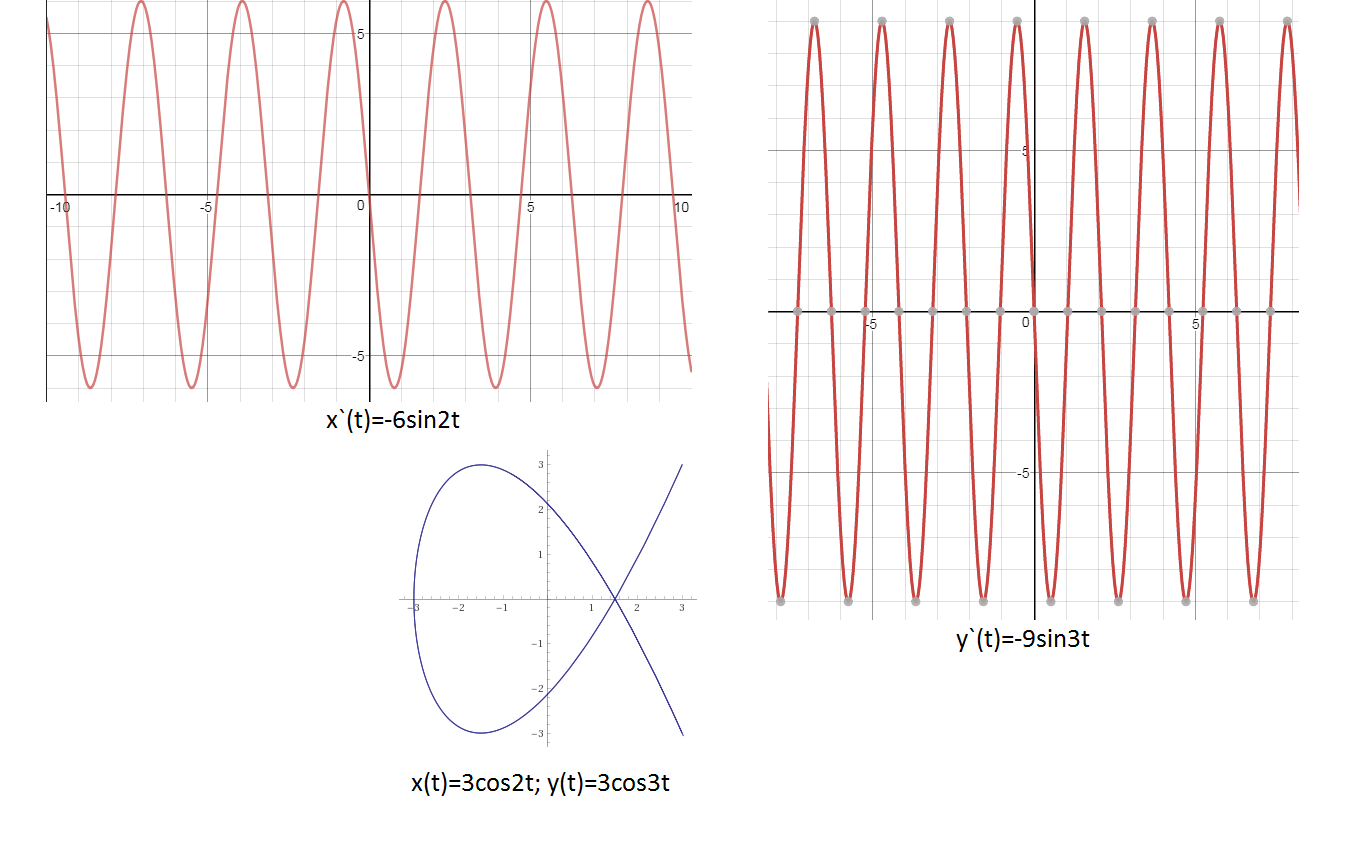
3) x = 3cos2t, y = 3cos3t

SOVA

6 октября 2018 г. в 00:00

1.
D(y)=(– ∞;– ∛–2)U(– ∛–2;+ ∞ )
y`=((x<sup>4</sup>)`·(x³+2)–x⁴·(x³+2)`)/(x<sup>3</sup>+2)<sup>2</sup>=
=(4x<sup>6</sup>+8x<sup>3</sup>–3x<sup>6</sup>)/(x<sup>3</sup>+2)<sup>2</sup>=(x<sup>3</sup>·(x<sup>3</sup>+8)/(x<sup>2</sup>+2)<sup>2</sup>
y`=0
x³·(8+x³)=0
x³=0 или x³+8=0
x=0 или x=–2

__+__ (–2) ___–___ (–∛–2) __–__ (0) __+__

Функция возрастает на (– ∞;–2) и на (0;+ ∞ )
убывает на (–2;–∛–2) и на (–∛–2;0)
х= –2 – точка максимума производная меняет знак с + на –
х=0 – точка минимума, производная меняет знак с – на +

см. рис. 1

2.
D(y)=(– ∞ ;+ ∞ )
y`=cosx+(1/2)(cos2x)·(2x)`
y`=cosx+cos2x
y`=0
cosx+cos2x=0
2cos²x+cosx–1=0
D=9
cosx=–1 или сosx=1/2
x=π+2πk, k ∈ Z или х= ± (π/3)+2πn, n ∈ Z

x=(π/3)+2πn, n ∈ Z – точки максимума
х=(–π/3)+2πn, n ∈ Z – точки минимума
х=π+2πk, k ∈ Z не являются точками экстремума.
см. рис. 2

3.
x`(t)= – 6 sin2t
y`(t)=– 9sin3t

Графики x`(t) и y`(t) cм. на рис. 3