Задача 28401 Вариант 2 1. Укажите промежутки...
Условие
1. Укажите промежутки возрастания и убывания функции
1) y = 2x^3 - 3x^2 - 12x + 1 | 2
2) y = ln x + 1/x | 1
2. Найдите критические точки
1) y = 2x e^x | 2
y = 2x e^x | 1
3. Найдите промежутки возрастания и убывания функции, точки максимума и минимума функции.
f(x) = 2x^2/(3 - x) | 2
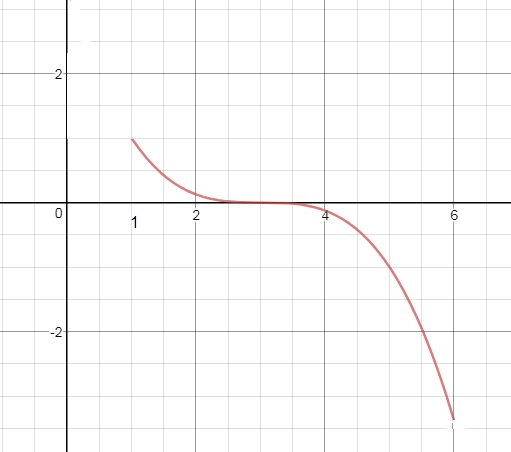
4. Постройте эскиз графика функции, удовлетворяющую условиям.
5. По графику функции найти промежутки возрастания и убывания функции, точки максимума и минимума функции.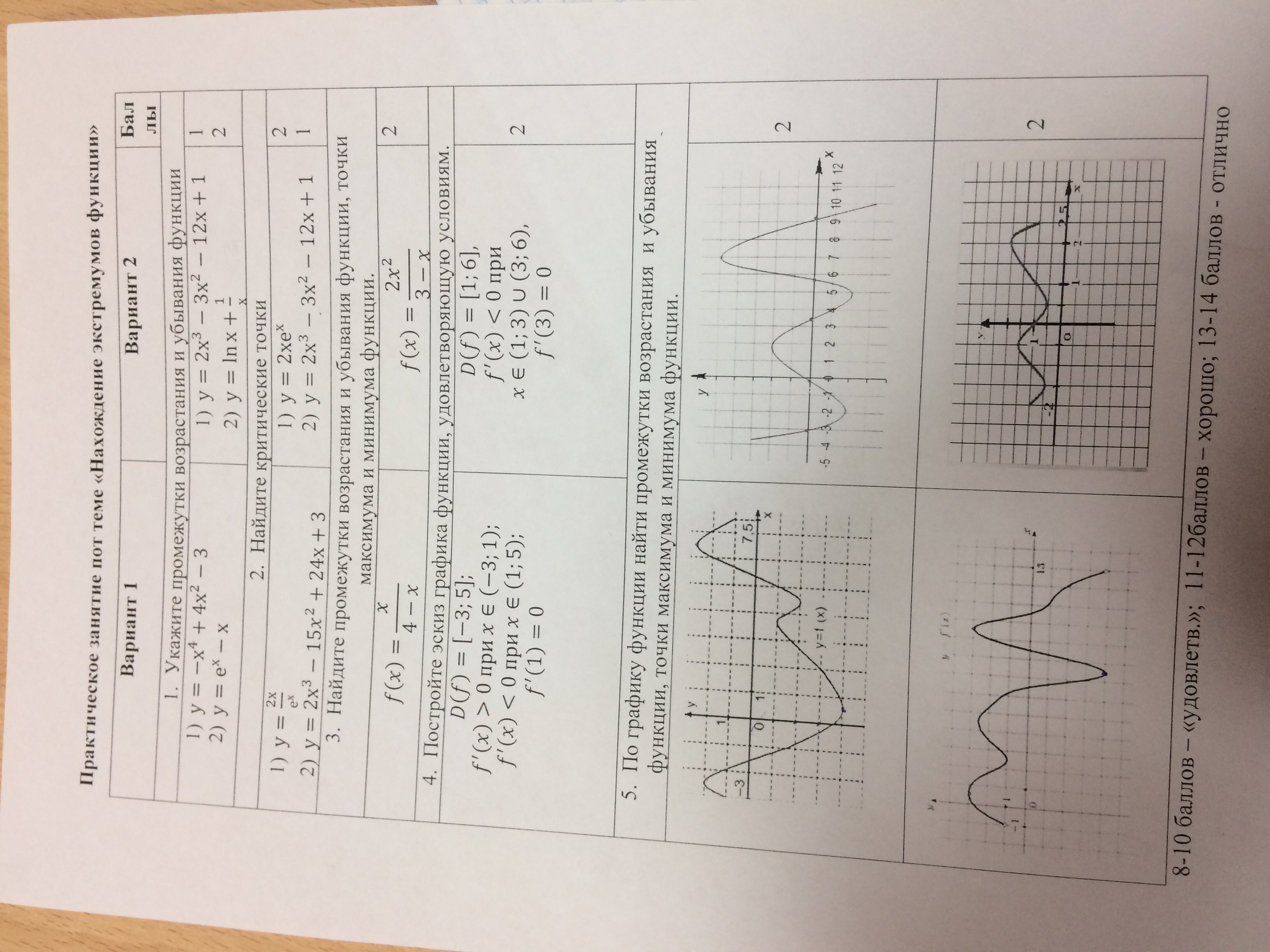
Все решения
а)D(y)=(- бесконечность :+ бесконечность )
y`=6x^-6x-12
y`=0
6x^2-6x-12=0
x^2-x-2=0
D=9
x=-1 или х=2
_+__ (-1) __-__ (2) _+__
возрастает на (- бесконечность ;-1) и на (2;+ бесконечность)
убывает на (-1;2)
б)
D(y)=(0;+ бесконечность )
y`=(1/х)-(1/х^2)
y`=0
(1/x)=(1/x^2)
x^2=x ( так как согласно ОДЗ х≠ 0)
x=1
(0) __-__ (1) _+__
убывает на (0;1)
возрастает на (1;+ бесконечность)
2.
а)D(y)=(- бесконечность :+ бесконечность )
y`=2*(x)`e^(x)+2x*(e^x)`=2e^(x)+2xe^(x)=2e^(x)*(1+x)
y`=0
e^(x) > 0 при любом х
1+х=0
х=-1 - критическая точка (вообще- то стационарная, в ней производная обращается в 0, в критической не существует)
б)
см.1 а
y`=0
x^2-x-2=0
x=-1 или х=2 - стационарные точки
3.
D(y)=(- бесконечность;3) U(3;+ бесконечность )
y`=((2x^2)`*(3-x)-(2x^2)*(3-x)`)/(3-x)^2
y`=2x*(6-x)/(3-x)
y`=0
x=0 или х=6
_+__ (0) ___-___ (3) ___-__ (6) __+___
возрастает на (- бесконечность ;0) и на (6;+ бесконечность)
убывает на (0;3) и (3;6)
х=(0) - точка максимума
y_(max)=y(0)=0
x=6- точка минимума
y_(min)=y(6)=-24
4.
см. рис.1
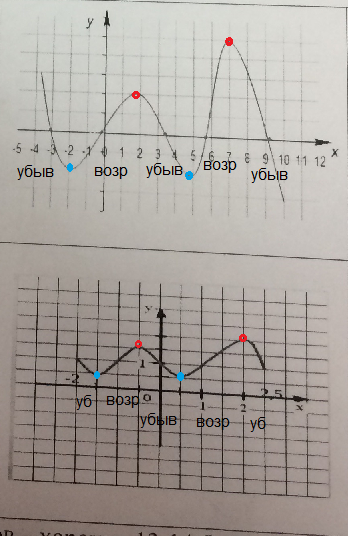
5.
см. рис. 2
а)
убывает на ( - бесконечность; -2) и на (2;4,9) и на
возрастает на (-2;2) и на (4,9;7)
х=2 и х=7 - точки максимума
х=-2 и х=4,9 - точки минимума
б)
убывает на ( - 2; -1,5) и на (-0,5 ; 0,5) и на (2; 2,5)
возрастает на (-1,5 ; -0,5) и на (0,5 ; 2)
х= - 0,5 и х=2 - точки максимума
х= - 1,5 и х=0,5 - точки минимума