Задача 28399 Вариант № 4 В1. Футболка стоила 800...
Условие
В1. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
В2. Шоколадка стоит 30 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 500 рублей в воскресенье?
В3. Найдите длину вектора [m]\vec{a} (-5,-12)[/m].
В4. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок с дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
В5. Решите уравнение [m]\sqrt{3 + 4x} = \sqrt{x}[/m]. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В6. Материальная точка движется прямолинейно по закону [m]x(t) = \frac{1}{4} t^4 + 3t^3 + 6t^2 + 7t + 11[/m] (где [m]x[/m] — расстояние от точки отчета в метрах, [m]t[/m] — время в секундах, измеренное с начала движения). Найдите её скорость (в м/с) в момент времени [m]t = 4с[/m].
В7 Прямая [m]y = 3x + 5[/m] является касательной к графику функции [m]y = x^2 + 7x - 5[/m]. Найдите абсциссу точки касания.
В8 На рисунке изображен график функции [m]y = f(x)[/m], определенной на интервале [m][-1;13][/m].
Определите количество целых точек, в которых производная функции положительна.
B9. На рисунке изображён график некоторой функции [m]y = f(x)[/m] (два луча с общей начальной точкой). Пользуясь рисунком, вычислите [m]F(7) - F(4)[/m], где [m]F(x)[/m] — одна из первообразных функции [m]f(x)[/m].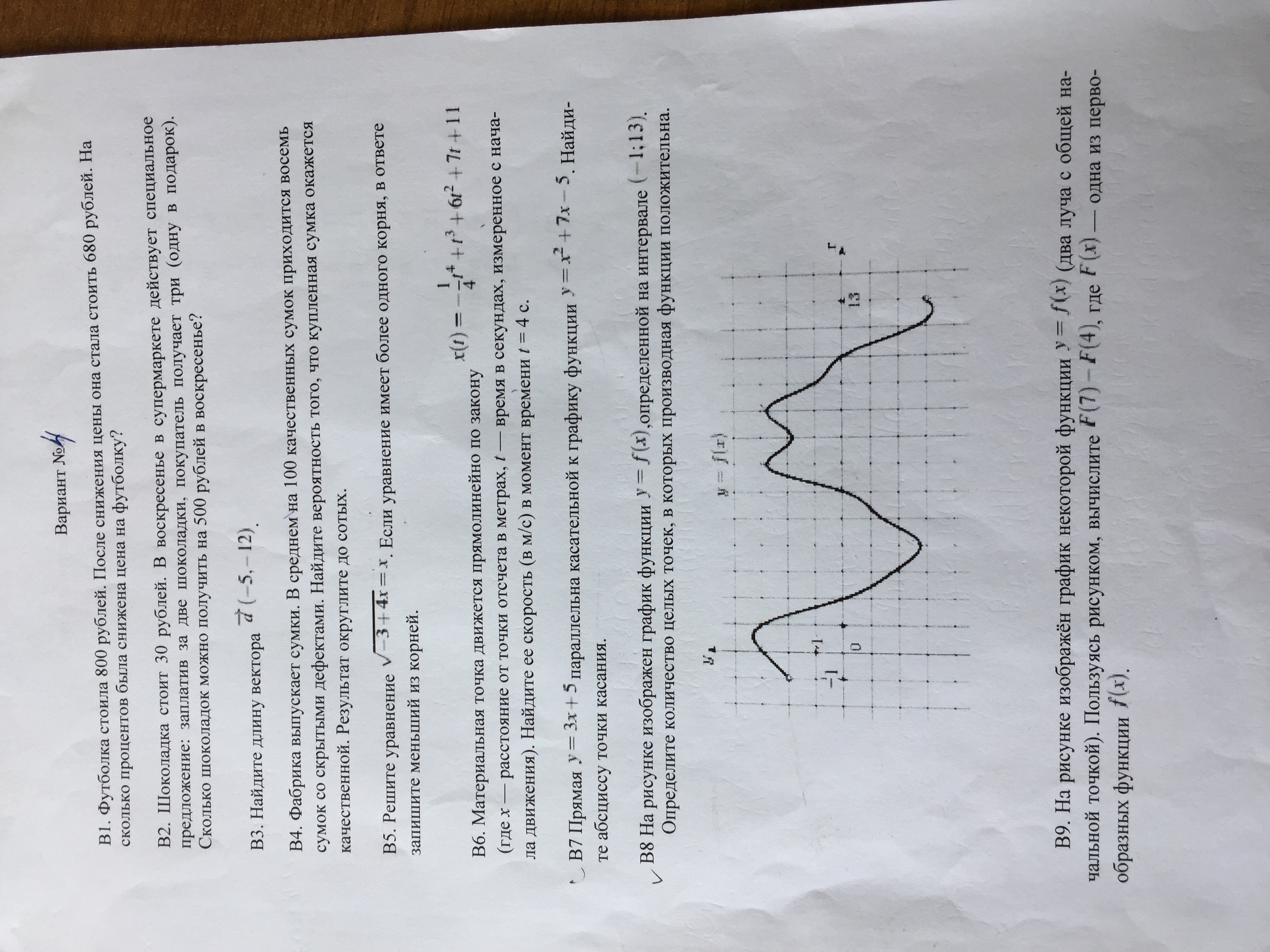
Все решения

