Задача 28373 ...

vk433259264

08.06.2018

1. Криволинейный интеграл второго рода и его вычисление.
2. Дифференцирование рядов и последовательностей.
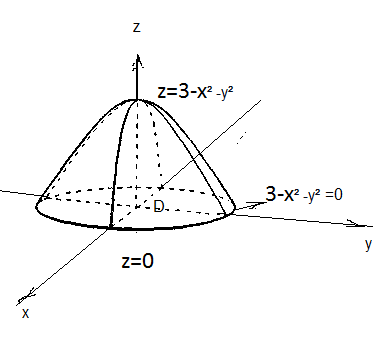
3. Вычислить объем тела, ограниченного данными поверхностями z = 0, z = 3 - x² - y².

SOVA

08.06.2018

★

V= ∫ ∫ _(D)(3-x^2-y2)dxdy
D:3-x^2-y^2=0 - круг радиуса sqrt(3) с центром (0;0)
Переход к полярным координатам
х=rcos phi
y=rsin phi
dxdy=rdrd phi
Тело симметрично относительно координатных плоскостей х=0 и у=0, поэтоу можно посчитать только (1/4) часть и умножить на 4
V= 4∫^(Pi/2) _(0) ∫^(sqrt(3) )_(0)(3-r^2)rdr=
=4*(Pi/2)*((sqrt(3)r^2/2)-(r^4/4))|^(sqrt(3))_(0)=
=2Pi*((3sqrt(3)/2)-(9/4))