Задача 28361 Вариант 2. 1. Двугранный угол при ребре...
Условие
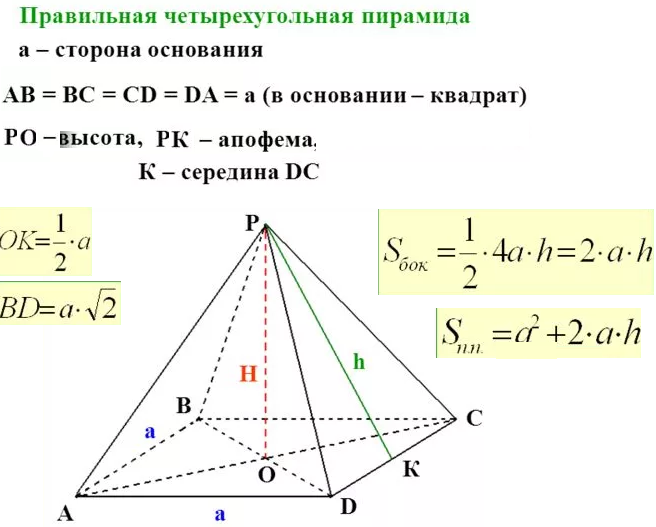
1. Двугранный угол при ребре основания правильной четырёхугольной пирамиды равен 30°, а апофема 10см. Найдите площадь основания.
2. Боковое ребро правильной четырёхугольной пирамиды равно 2см и наклонено к плоскости основания под углом 30°. Найдите:
1) высоту пирамиды;
2) радиус окружности, описанной вокруг основания;
3) диагональ основания
4) площадь диагонального сечения;
5) сторону основания;
6) радиус окружности, вписанной в основание;
7) площадь основания.
8) Объём.
Вариант 5.
1. В основании прямого параллелепипеда лежит ромб с диагоналями 24см и 10см. высота параллелепипеда равна 5см. Найдите:
A) площадь диагональных сечений;
Б) площадь боковой поверхности;
B) площадь полной поверхности.
2. Найдите диагональ прямоугольного параллелепипеда с измерениями 3см, 8см, 10см.
3. Каждая грань параллелепипеда ромб со стороной 10см и углом 30°. Найдите площадь полной поверхности параллелепипеда.
Все решения
∠ PKO=30 градусов;
PK=10
Из прямоугольного треугольника РКО:
ОК=10*cos30 градусов=10*sqrt(3)/2=5sqrt(3) см
ОК=(1/2)*a ⇒ a=10sqrt(3) см
S(осн.)=S(квадрата)=a^2=(10sqrt(3))^2=300 кв см
2.
PA=PB=PB=PD=2 cм
∠ РАО= ∠ РВО= ∠ РСО= ∠ РDО=30 градусов
Катет против угла в 30 градусов равен половине гипотенузы.
а)PO=H=1 cм - высота пирамиды
б)
R=АО=ОС=ОB=OD=2*cos30 градусов=sqrt(3)
3.
d=АС=BD=2R=2sqrt(3)
4.
S(диагонального сечения)=(1/2)*АС*PO==(1/2)*2sqrt(3)*1=sqrt(3)
5,
d^2=a^2+a^2=
2a^2=(2sqrt(3))^2
2a^2=12
a^2=6
a=sqrt(6)
6.
r=a/2=sqrt(6)/2
7.
S( осн)=a^2=(sqrt(6))^2=6
8.
V=(1/3)S(осн.)*Н=(1/3)*6*1=2