Задача 28308 Задача 1. В правильной четырехугольной...

u80832373

6 мая 2018 г. в 00:00

Задача 1. В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 20, BD = 30. Найдите боковое ребро SC.

Задача 2. Найдите площадь полной поверхности правильной четырехугольной пирамиды, если высота ее равна 20 см, а длина стороны основания 42 см.

Задача 3. Дан прямоугольный параллелепипед с линейными измерениями 5 см, 7 см и 10 см. Найдите диагональ параллелепипеда.

SOVA

6 мая 2018 г. в 00:00

1.
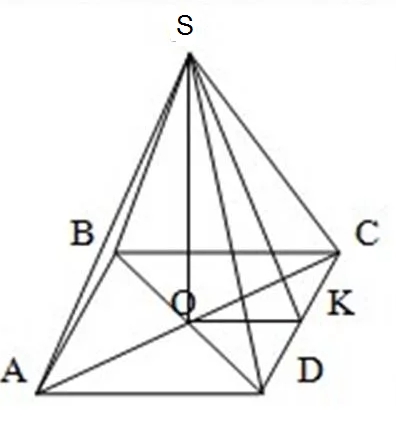
Диагонали квадрата ABCD равны, в точке пересечения делятся пополам ( cм. рис.)
OB=OD=15

По теореме Пифагора из прямоугольного треугольника SOB
SB²=SO²+OB²=20²+15²=400+225=625
SB=25

2.
АВСD– квадрат
AB=BC=CD=AD=a

SK=h – апофема пирамиды ( или высота боковой грани)

По теореме Пифагора из прямоугольного треугольника SOK ( см. рис. ОК=1/2 АВ=a/2)
SK²=SO²+OK²=20²+(21)²=400+441=841
h=SK=29
S=S(осн.)+S(бок)=a²+(4a·h/2)=42²+84·29=4200 кв см

3.
По формуле
d²=a²+b²+c²

d²=5²+7²+10²
d²=25+35+100
d=√160=4√10