Задача 28259 ...
Условие
математика ВУЗ
707
Решение
★
s(длина дуги)= ∫ βα √1+(x`(y)2)dy
x=2y2
x`=4y
1+(x`)2=1+(4y)2=
s(длина дуги)= ∫ 20 √1+4y2dy=
[ интегрируем по частям или находим готовую формулу 18.
[b]u=2y[b]]
=(y·√1+4y2+ln|2y+√1+4y2|)|20=
=2·3+ln(4+3)=6+ln7
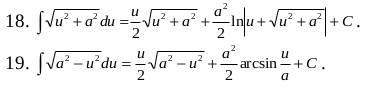
Обсуждения