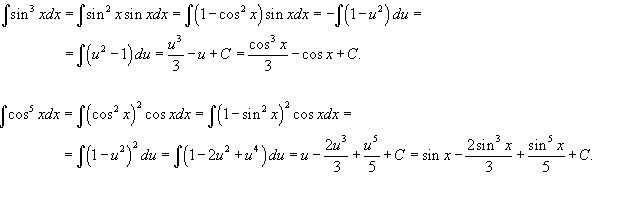Задача 28166 ...
Условие
23. Вычисление интегралов типа ∫ℝ(cos x)sin xdx.
24. Вычисление интегралов типа ∫ℝ(lg x)dx.
25. Вычисление интегралов типа ∫sin^m x·cos^n xdx.
26. Примеры вычисления интегралов типа ∫sin^m x·cos^n xdx в случае непарных положительных значений m и n.
Решение
Замена переменной ( подстановка)
sinx=t
сosxdx=dt
23.
Замена переменной
cosx=t
-sinxxdx=dt ⇒ sinxdx=-dt
24.
Замена переменной
tgx=t
x=arctgt
dx=dt/(1+t^2)
25.
Если показатель одной из тригонометрических функций ( m или n) - нечетное число, то другую функцию принимаем за t ( как в 22 и 23)
Если
m+n- четное, то подстановка tgx=t
Если
m и n - четные неотрицательные, формулы понижения степени
sin^2x=(1-cos2x)/2; cos^2x=(1+cos2x)/2
26
В случае m и n - нечетные положительные
cм. приложение