Задача 28117 ...
Условие
1. Вычислите sin α, если cos α = -0,2, α ∈ II четверти
2. Решите уравнение:
1) 2 sin x - √3 = 0;
2) tg x + √3 = 0
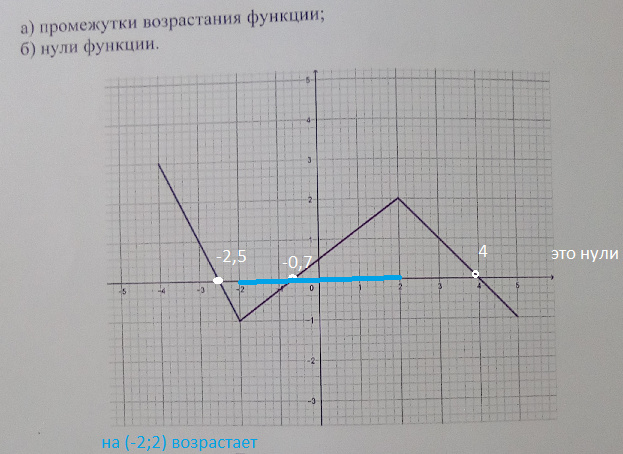
3. Найдите по графику
а) промежутки возрастания функции;
б) нули функции.
Дополнительная часть
4. Решите уравнение:
2 cos x = 1 + cos 2x
5. Записать уравнение касательной к графику функции
f(x) = sin x - 3x + 2, в точке x₀ = 0.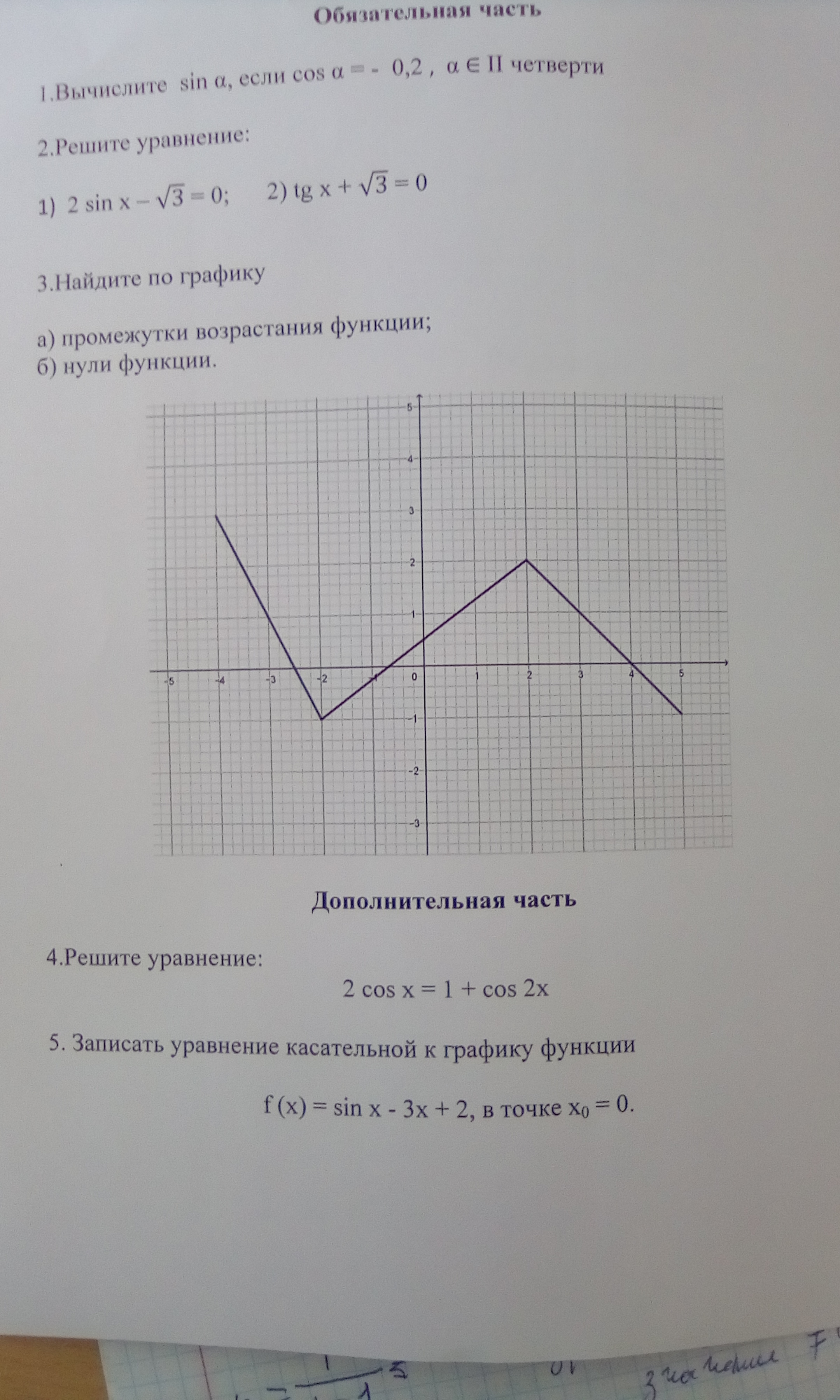
Все решения
sin^2 альфа +cos^2 альфа =1 ⇒ sin альфа = ± sqrt(1-cos^2 альфа )
Так как угол во второй четверти, синус во второй четверти имеет знак +
sin альфа =+sqrt(1-(0,2)^2)=sqrt(1-0,04)=sqrt(0,96)=0,4*sqrt(6)
2.
sinx=sqrt(3)/2
x=(-1)^karcsin(sqrt(3)/2)+Pik, k ∈ Z
x=(-1)^k*(Pi/3)+Pik, k ∈ Z - о т в е т.
tgx=-sqrt(3)
x=arctg(-sqrt(3))+Pin, n ∈ Z
x=(-Pi/6)+Pin, n ∈ Z
3.