Задача 28098 4.3.4) Найти уравнение окружности,...

slava191

29.05.2018

4.3.4) Найти уравнение окружности, касающейся осей координат и проходящей через точку (4; -2).

SOVA

29.05.2018

★

Окружность касается осей координат и проходит через точку, расположенную в четвертой координатной четверти, значит центр окружности лежит на биссектрисе второго и четвертого координатных углов, т.е на прямой y = - x.
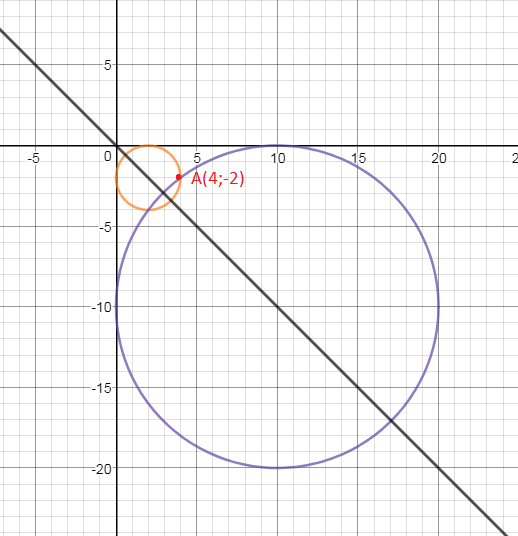
и потому центр окружности имеет координаты (R;-R)

Следовательно, уравнение окружности имеет вид
(x - R)^2 + (y -(- R))^2 = R^2.

Поскольку точка A(4;-2) лежит на окружности, координаты этой точки удовлетворяют полученному уравнению,
т.е.
(4 - R)^2 + (-2 + R)^2 = R^2.
16-8R+R^2+4-4R+R^2=R^2
R^2-12R+20=0
D=144-80=64
R=2 или R=10

(x - 2)^2 + (y+2)^2 = 4 или
(x - 10)^2 + (y+10)^2 = 100

.