Задача 28094 9.56. Зная медианы треугольника, найдите...

slava191

29.05.2018

9.56. Зная медианы треугольника, найдите его площадь.

SOVA

29.05.2018

★

Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.

Медиана делит треугольник на два равновеликих треугольника
S (Δ ABH)= S( ΔBCH)

S( ΔАОС)=(1/3) S ( Δ АВС)

S (Δ AОH)= S( ΔCОH)

S( ΔАОН)=(1/6) S ( Δ АВС)

Все три медианы делят треугольник на 6 равновеликих треугольников.

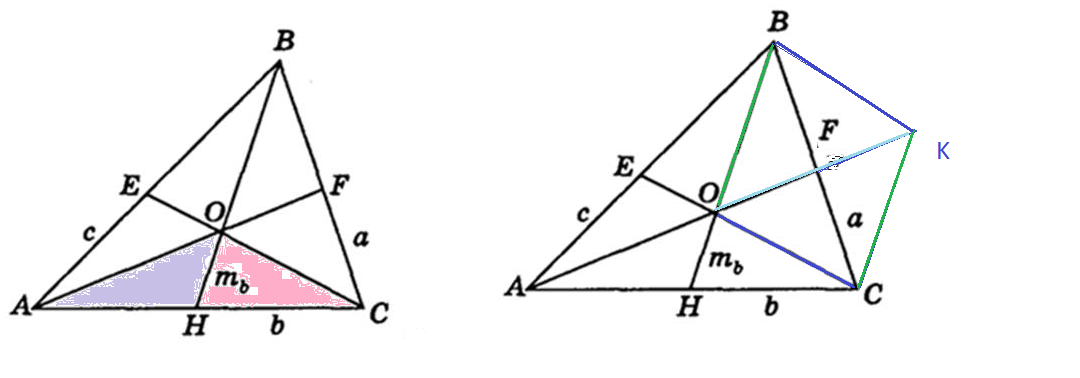
[b] Дополнительное построение [/b]

Продолжим медиану AF за точку F на (1/3) ёё длины.

Получим параллелограмм ОВКС,
S(ОВКС)=2S(Δ ОВК)

S(Δ ОВК)=(2/6)S(Δ AВC)

Значит, площадь треугольника АВС найдем, зная площадь треугольника ОВК.

ОВ=(2/3)m_(b)
ВК=(2/3) m_(с)
ОК=(2/3)m_(a)

В треугольнике ОВК известны все стороны.
Значит можно найти площадь по формуле Герона

p=(1/3)(m_(a)+m_(b)+m_(c))
р-а=(1/3)(m_(a)+m_(b)+m_(c))-(2/3)a=
(1/3)((m_(b)+m_(c)-m_(a))
p-b=(1/3)(m_(a)+m_(b)+m_(c))-(2/3)m_(b)=
=(1/3)(m_(a)-m_(b)+m_(c))
p-c=(1/3)(m_(a)+m_(b)+m_(c))-(2/3)m_(c)=
=(1/3)(m_(a)+m_(b)-m_(c))

S( Δ ОВК) =(1/9)sqrt((m_(a)+m_(b)+m_(c))*((m_(a)+m_(b)-m_(c))(m_(a)-m_(b)+m_(c))(m_(b)+m_(c)-m_(a))))

S( Δ АВС)=3*S( ОВС)=
=(1/3)sqrt((m_(a)+m_(b)+m_(c))*((m_(a)+m_(b)-m_(c))(m_(a)-m_(b)+m_(c))(m_(b)+m_(c)-m_(a))))

Пусть
(m_(a)+m_(b)+m_(c))/2=m, тогда
m_(a)+m_(b)+m_(c)=2m
m_(a)+m_(b)-m_(c)=2*(m-m_(c))
m_(a)+m_(c)-m_(b)=2*(m-m_(b))
m_(b)+m_(c)-m_(a)=2*(m-m_(a))

S( Δ АВС)=3*S( ОВС)=
=(1/3)sqrt((m_(a)+m_(b)+m_(c))*((m_(a)+m_(b)-m_(c))(m_(a)-m_(b)+m_(c))(m_(b)+m_(c)-m_(a))))=
=(4/3)sqrt(m*(m-m_(a))*(m-m_(b))*(m-m_(c)))

О т в е т. (4/3)sqrt(m*(m-m_(a))*(m-m_(b))*(m-m_(c)))
Так формула лучше просматривается, есть сходство с формулой Герона.